|
�����̘b�ƃM�^�[�ł̎���
�s�^�S���X�̊��L�@�@�@���F��؏�
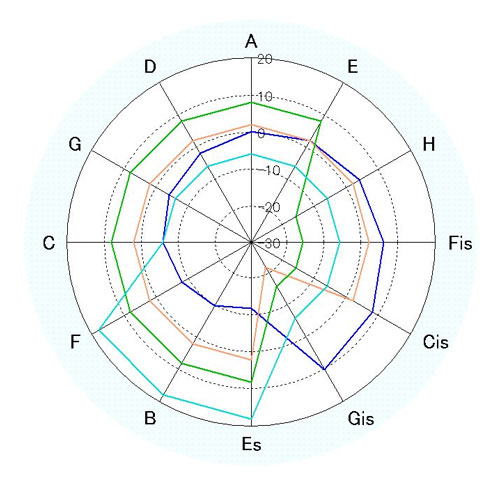
�s�ܓx�����[�_�[�}�F�s�^�S���X�����t
�M�^�[�t�҂��m���Ă������������̒m��
�͂��߂�
�u�������āA���K�̂��Ƃł��傤�v�Ǝv���Ă���l���ĊO�����Ǝv���܂����A��܂��ɂ͐������悤�ł����A���m�ɂ͐����Ⴄ�ƌ������ق��������ł��傤�B
���y���y���ނ��߂ɂ͉��K���K�v�ł��B�����Ȃ肱��Ȃ��Ƃ������ƁA�O�q���y�̎�����������ė����l�B����́A�������Ƀu�[�C���O�������ł����A��ʓI�ɂ͊y���Ƃ��Ď��g���̊m�肵�����ō\�����ꂽ���K���g�������y���J�ɂ͈��Ă��܂��B���̉��K���ǂ����������ō\���������������ł��B
�����ďo�������̂����K�ƌ������ق��������ł��傤�B
���y���T�������Ɓu���y�Ŏg�������W�������w�I�E���w�I�ɋK�肵�����́v�������ł��B
�����āu����ɉ����Ċy��̉��������肷�邱�Ƃ��Ƃ����v�̂������ł��B�����牽�ł���Șb������̂��ƌ����ƁA�����̘b�肪�ʔ�������ł��B�����̗��j�͉��y�̗��j���̂��̂ƌ����Ă����������m��܂���B
�l�����y������悤�ɂȂ��Ăǂ̂��炢�̎��Ԃ��o�����̂�������܂��A���Ȃ��Ƃ��������N���Ă���A���������̖��͔������Ă������낤�Ǝ��͎v���܂��B
�Ñ�o�r���j�A�����ł̓n�[�v�̂悤�Ȋy��̒����������ܓx�ōs���Ă������Ƃ��A�������̉�ǂɂ���ĕ������Ă��邻���ł��B��l��N���̂̂��Ƃł��B�����Č���͕��ϗ�����ʓI�Ɏg���Ă��āA���ɃM�^�[�̂悤�Ƀt���b�g�����y��ɂƂ��ẮA���̉����͐�ΓI�Ȃ��̂��ƌ����Ă������ł��傤�B���ϗ��̓o��ʼn������͉����������Ɏv���܂������A�ǂ��������ł͂Ȃ��悤�ł��B�_���ȋ�������������������߂ẮA�O���Ȃ��T���S����藧�Ă�Փ��Ȃ̂����m��܂��A�ނ��떢���i�������������ɂȂ��i���̃e�[�}�Ȃ̂����m��܂���B�V���ȉ��������܂�邱�ƂŁA���̎���̉��y���傫���ω����Ă����ߒ������y�̗��j���Ƃ������܂��B�����Č��݂͂Ƃ����ƁA�����Ŕ��W���Ă������y���O�q�̎�����߂��A�s����������ĕY�����Ă���悤�Ȓ����[�h�����锽�ʁA���Ɖ��y�͉v�X����ɂȂ��Ă��܂��B
�N���V�b�N�ƃ|�s�����[�̋�ʂ��Ȃ��Ȃ��Ă����̂��A������������w�i�Ɩ��W�ł͂Ȃ��悤�Ɏv���܂��B
�����̘b��͕��i�͂��܂�\�ɏo�Ă��Ȃ����̂ł����A���̉��y�̖{���Ƃ������ׂ��e�[�}�𑽏��̒m���Ƃ��Ď����Ă��Ă��A�����邱�Ƃ͂Ȃ����낤�Ƃ������ƂŎ��グ�Ă݂����Ǝv���܂��B
�����̎��
��ȉ����̖��O��������A���ϗ��A�������A�s�^�S���X�����A���S�����i�~�[���E�g�[���j�A�e��̌܉����K�i�y���^�E�g�j�b�N�j�̑��ɂ��A �s�A�m���̌��Պy���NJy��ł́A���F���N�}�C�X�^�[�A�L�����x���K�[�A���@���b�e�B�i�����O�j�A�P���i�[�����m���Ă��܂����A�o�b�n���s�Ȃ��Ă������������̂悤�Ȏ�ނ̒����������悤�ł��i�Q���j�B���ϗ��ɂ��ẮA���{�ł́u���ϗ��N�����B�[�A�ȏW�v���������o�b�n������������̂悤��
�v���Ă��܂������A�o�b�n�͕��ϗ����g���Ă��Ȃ��������Ƃ����݂ł͖��炩�ɂȂ��Ă��܂��B���ϗ��������I�Ɏ����ꂽ�̂̓o�b�n�̏����O�̎���ŁA�ΐ��\���n��ꕡ�G�Ȍv�Z���ł���悤�ɂȂ������Ƃ���Ԃ̗v�f�ł��B
��̓I�Ȓ������@�Ƃ��Ĕ��\�����̂̓����Z���k�ŁA�t���b�g�����y��ɂ͗L���ł���Ƃ��āA�t���b�g��Ő݂���ʒu�𐔒l�ŕ\�����̂��ŏ��̂悤�ł��i���P�j�B
�����̉����͎�ɉ��B�Ɍ�������̂ŁA���̑��ɂ��A���u��C���h�̃A�W�A�ł͑S���قȂ鉹�����g���Ă��܂����A���̑��̒n��ɂ��Ɠ��̂��̂����݂��܂��B���B���g���Ă��镽�ϗ��́A�������{���ߑ㉻��i�߂邽�߂ɁA���m����ڎw���ĉ��Ă���{�Ɏ���ꂽ���̂ł��B����ȑO�͒�������`����ꂽ�u�O�����v�@�v�ɂ��s�^�S���X�������g���Ă��܂����B
���q�@�ɂ͒�������`������Êy�킪��������c����Ă��܂����A�O�����v�@�ɂ�鉹�K���g���Ă������̂Ɛ�������܂��B
���{�ł͌Â����珇���t�Z�Ƃ������@���g���Ă����悤�ł����A����͎O�����v�@�Ɠ����ł�������{�̉��K�͕����蓾��͈͂ł̓s�^�S���X���K����̂ł��B���̃M���V���Ő��܂ꂽ�s�^�S���X�����́A���R�Ƀ��[���b�p�ł������܂ł͎g���Ă���܂����B�O���S���I���̂̓s�^�S���X���K���g���A�P�����ʼn̂��܂��B
����͓Ɠ��̕��͋C������A���{�ł����Â��Ȑl�C������悤�ł��B
����̉����̘b�͂��̐����Ŕ��W���������ɂ��Ă݂̂ł��B���͂���ȊO�̉����ɂ��ẮA���͕s���ŕ�����܂���B�F�X�Ə��Ђ��o�Ă���ł��傤����A�\����܂������̂�����͂���������ĉ������B���̋L���ł̖ڕW�́A�M�^�[��e���҂Ƃ��Ă̗��ꂩ��A���炩�̋�̓I�Ȏ��H�Ƃ��ĉ����̒m�������p�ł��Ȃ����Ƃ����_�ɂ���A�܂�������ʂ��ăM�^�[�����߂Ă݂悤�Ǝv���܂��B���̏�Ō��݂̉��y�����ꂩ��ǂ̂悤�ɐi��ł����̂��A�����̘b�肩��M�^�[�̖�����z�����Ă݂����Ǝv���܂��B
�\���m��
���鉹���P�I�N�^�[�u�������͐U�������Q�{�ɂȂ�܂��B�ł�����A�Q�I�N�^�[�u�ł͂S�{�ɂȂ�܂��B�����Ă����̉��ɂ͉����̈Ⴂ�����邱�Ƃ͏��m�̏�ŁA���o�I�ɂ͓������Ƃ��ė�������Ă��܂��B�����̈Ⴂ�͐U�����̔䗦�ŕ\�킷���Ƃ��ł��A����1�I�N�^�[�u�̉������䗦�ŋϓ��ɂP�Q���Ɋ��������ō\���������̂����ϗ��ł��B�܂艹���͐U�����Ƃ������_�ł݂�ƁA�|���Z����̂ƂȂ��Ăł��Ă��āA�����̐U��������P�Q��|�����킹��ƂQ�ƂȂ�A1�I�N�^�[�u�����Q�{���ɂȂ�܂��B���̔������P�O�O���������������P�Z���g�Ƃ����܂��B�ׂ��ȉ�����\������ɂ͂��̃Z���g�\�����������܂���̂Ŋo���Ă����ĉ������B
����A�Q�̉����ɖ炵�����̋��a���鋿���͔{���Ƃ��Ă̊W�ɂȂ�܂��B��ʂɂ͈�̉�����ƁA���̐U�����ɑΉ����Ă��̂Q�{���A�R�{���A�T�{���c�Ƌ����ۂ��N�����Ė荇�킳��A���̎��ɔ{�����������������傫�ȉ��Ƃ��ċ����܂��B
�M�^�[�Ŏ������Ă݂�ƁA�@���̊J������e���ƇE���ƇD���̊J���������U�����܂��B�@�����������Ă��E�D���͖葱���܂��B�X�ɇE������������ƇD�����������Ă��邱�Ƃ�������܂��B���ꂩ�猷�̒����ƐU�����̊W�͔���Ⴕ�܂��̂ŁA�M�^�[�ł݂�ƌ����̐^�����P�Q�t���b�g�ɂȂ��Ă��āA�J������1�I�N�^�[�u�������ɂȂ��Ă��܂��B�U�����錷�̒����������ɂȂ�A�U�������Q�{�ɂȂ�܂��B���̂��Ƃ͊��Ƀo�r���j�A�̎��ォ��m���Ă���܂������A���p�O�p�`�̒藝�ŗL���ȃM���V���̃s�^�S���X�͉����̌��������邽�߂ɁA���m�R�[�h�i�ꌷ�Ձj�Ƃ����������g���Ă��܂����B
�܂�����͍\���I�ɃM�^�[�̃t���b�g��{�[�h�Ǝ����悤�Ȃ��̂ŁA���m�ȉ����𑪂�ɂ͍ł��D�ꂽ���̂������悤�ł��B������C�̐U���ł���Ƃ������Ƃ��������Ă��Ȃ���������ł�����A���̒�����J�̒����ƌ��̈ʒu�Ȃǂʼn��������������킯�ł��B�s�^�S���X�ȍ~�����������ł̓��m�R�[�h�ɂ���čs���A���m�R�[�h���ǂ̂悤�Ȓ����̔䗦�ɕ������邩�Ƃ������m�R�[�h�����Ƃ�����@�ŁA���l�T���X����̏������̌����ɂ����S�I�Ȗ������ʂ����Ă��܂��B�܂�M�^�[�͉����������ɂ͓K�����y�킾�ƌ����܂��B
�{���Ə����ȋ���
�{���W�ɂ��鉹���ɖ炷�ƁA���S�ɂƂ����������������܂��B���ϗ��ɂȂ�Ă��܂������B�̒����o���炷��ƁA�ނ���M���M���Ƃ������ɐH�����ނ悤�Ȃ������������邩���m��܂��A�̂��炱�ꂪ�������Ǝv���Ă��������ȋ����ł��B�܂�U�������ȒP�Ȑ�����ŕ\�����Ƃ��ł��鉹���W�ɂ���܂��B�M�^�[�Ŕ{���𗝉������ԗǂ����@�͎��R�n�[���j�b�N�X�ł��B�����ƐU�����錷�̒���������Ⴕ�Ă��邱�Ƃ��ڂł�������܂��B�Q�{���͂P�Q�t���b�g�Ŕ����A�R�{���͂V�A�P�X�t���b�g��1/3�ł��B�S�{���͂T�t���b�g�A�T�{���͂S�A�X�A�P�U�t���b�g�ƂȂ�܂��B�V�{���ȍ~�͉��K�Ƃ��ẴY�����傫�����߂Ƀt���b�g��ł͂Ȃ��Ȃ��Ă��܂��܂��B
���B�M�^�[�t�҂͂T�{���n�[���j�b�N�X���t���b�g�ʒu���班���Y���Ă��邱�Ƃ��o���I�ɒm���Ă��܂����A���͂��̎��������������̗��j����������{�l�ł�����Ƃ������Ƃł��B���̔����ȃY�������ꂩ��̘b��ƂȂ鐔�X�̉������̂ŁA�T�{���̏h���Ƃ������ׂ����ԂȂ̂ł��B
�M�^�[�̃t���b�g�͕��ϗ��ō���Ă��܂�����A�܂肱�̃Y�������ϗ��Ə������̉������Ƃ������Ƃł��B
�����Ŕ{���Ɖ����Ƃ̊W���͂�����������Ă����܂��傤�B���ɂ������̕��������Ǝv���܂����A�������t�������������B�Q�{���͂P�I�N�^�[�u�������ł��B�h�̉�����ɂ���ƂR�{���̓\�̉��ł����A�Q�{�������X�ɍ����̂ŁA���K���P�I�N�^�[�u�̒��ɂ܂Ƃ߂�ɂ́A�P�I�N�^�[�u������1/2�{���邱�ƂɂȂ�܂��B1�I�N�^�[�u�̉��K�̒��ł͊��S5�x��3/2�{���ł��B���̃\�̉����X�ɂR�{����i�\���T�x��������j�ƃ��ł����A��͂�I�N�^�[�u�̒��ɂ��낦�邽�߂ɂ́A�Q�I�N�^�[�u������9/8�ƂȂ�܂��B�����ŋt�ɂR�{���̃\��1/3�{����ƁA�P�Q�x�������Ċ�̃h�ɂȂ�܂��B�����łS�{���̃h��1/3�{����ƂP�Q�x���̃t�@�ɂȂ�A���4/3�{�̃t�@�ƂȂ�܂��B�i����P�j
����P�@�R�{���n��

���͕���Q�Ɏ����T�{���ł����A�Q�I�N�^�[�u�{���R�x�̃~�̉��ł��B�ł�����Q�I�N�^�[�u������5/4�{�ƂȂ�܂��B����Ɠ��l��1/3�{����ƃ��̉��ɂȂ�܂��B���Ƀ~�̉����R�{����ƃV�̉��ɂȂ�܂��̂ŁA�I�N�^�[�u�����Ď��߂܂��ƁA�������̃n�����_�C�A�g�j�b�N�X�P�[���̊����ł��B�i����R�j
����Q�@�T�{���n��

����R�@�������̑S���K�I���K
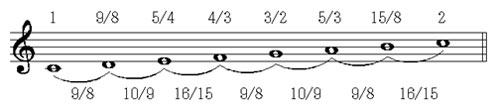
���̂悤�ɁA�����e����������ƑS����2��ޑ��݂��܂����A�傫������
��S���i9/8�j�A�������������S���i10/9�j�Ƃ����܂��B
�ϓ��ȉ����̕��ϗ�
����ɑ��āA�S�Ă̔������䗦�i�Q�̂P�Q�捪�j�ɂ����̂����ϗ��ł�����A�S����1��ނ�������܂��A�Z���g�ŕ\������ƑS���̉����P�O�O�Z���g�P�ʂɂȂ��Ă��܂��B����Ή����́u���̂����v�ƌ����ׂ����̂ł�����A
���̘b��i�߂��ŁA���ϗ����K�Ɍ����ĂĊe��̉������r�������Ǝv���܂��B
�@
���̂悤�ɕ��ϗ��͔����̔䗦�i1.059463����j�������Ȃ��������ŏo���Ă��܂�����A��ɔ{���n��ɂ͊܂܂�Ȃ����̏W���̂ƂȂ��Ă��܂��̂ŁA�����ȋ����Ɣ�ׂ�Ɣ������Ȃ��Ƃ������ƂɂȂ�܂��B�����̔��������������I�ȍ��������̗p�����������ƌ����܂��B
����ł́A�������Ƃǂ̂��炢�̈Ⴂ�����邩�Z���g�l�Ō��Ă݂�ƁA�\1�̂Ƃ���ł��B
�\�P�@���ϗ��Ə������̃Z���g�l

�l�̒��o�ʼn����������邱�Ƃ��ł���̂͂Q�`�R�Z���g�����x�������ł����A����͐����Ƃ��ĕ������ꍇ�ƁA�a���Ƃ��ĕ������ꍇ�Ƃł͋�����m�o����\�͂ɈႢ������܂��̂ŁA�������������ċ����̗ǂ�������P���ɔ��f�ł��Ȃ��Ǝv���܂��B
�s�A�m�����t�̎����ɂ����Ă͂T�Z���g�ȓ��ɒ������邱�Ƃ����߂��Ă���悤�ł����A�a���Ƃ��Ē��������͂R�Z���g���炢�܂ł͈Ⴂ�������邻���ł��B�M�^�[�̒����ł͂Q�Z���g�̈Ⴂ�����͒������Ă������ł��B
����������ȑO�ɁA�M�^�[�̃t���b�g�����m�ɐݒu����Ă��邩�A���̑������ψꂩ�A���������肵�Ă��邩�����d�v�ȃ|�C���g�ɂȂ�܂����A���̉������͎������̐��\�≷�x�⎼�x�̕ω��A�X�Ɍ��̐V���ł̐L�т̈Ⴂ���ŁA�܂������Ԃɕω����Ă��܂����̋ɂ߂ċ͂��ȈႢ�ł��B
�ŋ߂͓d�q�`���[�i�[���g�p���Ă���l�������Ǝv���܂����A���̃`���[�i�[�͍Œቹ�������Q�Z���g���炢�ł͂Ȃ����Ɗ�������@�킪�����悤�Ɏv���܂��B����ɑ��Đ����I�ɂ͂P�O�Z���g���炢�̈Ⴂ�͋��e�͈͂ɂ���Ǝv���܂��B�ܘ_���t�̘a������Ȃ���Ƃ������Ƃł��B
�����ň�Ԗ��ƂȂ��Ă��鉹�����~�ƃ��̂R�x�U�x�����ŁA���ϗ��ł͏��������ɑ��ĂR�x�͂P�S�Z���g�A�U�x�ł͂P�U�Z���g���Ⴄ���Ƃł��B���̉��������e���邱�Ƃŕ��ϗ����g���Ă��邱�ƂɂȂ�܂��B����Ɉ��������S�T�x�Ɗ��S�S�x�ł͂Q�Z���g�̈Ⴂ��������܂���̂ŁA������͑�ϔ������������ƂɂȂ�܂��B�܂蕽�ϗ��͂R�{���n��̉����Y��ɋ����܂����A�T�{���n��̋������ǂ��Ȃ����ƂɂȂ�܂��B���̂ǂ������邩�Ŋe��̉���������A���j�̗��ꂪ�`������邱�ƂɂȂ�܂��B
�s�^�S���X����
�����ŌÂ����烈�[���b�p�Ɍ��炸�A���E�̍L���n��Ŏg���Ă����s�^�S���X�����ɂ��Č��Ă݂܂��傤�B�s�^�S���X�͐������F�����x�z���Ă���ƍl���Ă����悤�ŁA�����𐔗��I�ɓ��ꂵ�����@�ō�邱�Ƃ��l���܂����B
�����č��ꂽ�������R�{������ɂ����s�^�S���X�����ł��B
�����R�{�������̊��S�T�x�Ŏ��X�Ɖ����d�˂Ă����ƁA�P�Q��ڂłV�I�N�^�[�u�ɂȂ�܂��̂ŁA���̂P�Q�̉����I�N�^�[�u�ϊ����āA������1�I�N�^�[�u���ɕ��ׂ����̂����K�Ƃ��Ďg�p����܂��B���g�����ɂ����1�I�N�^�[�u���̓������ɂȂ�A���������Ⴍ�Ȃ�Ȃ��Ƃ���܂ʼn����A���I�N�^�[�u����Ă��Ă��������Ɣ��f�����ł��B�Ƃ��낪�����Ŗ�肪�c��܂����B���S��7�I�N�^�[�u�ł͂Ȃ��A�Q�S�Z���g�i���m�ɂ͂Q�R�D�S�U�Z���g�j�I�[�o�[���Ă��܂������Ƃł��B���̉����̍����s�^�S���X�E�R���}�ƌ����܂��B
���ϗ��ł͂��̃R���}���P�Q�������Ċe�T�x�������Q�Z���g�Âk�߂Ă����ł��B�ł�����\1��G���V�O�Q�Z���g�̏������ɑ����ϗ��ł͂V�O�O�Z���g�ɂȂ��Ă��܂��B
�s�^�S���X�����͗��_�l�����܂���̂ŁA���̃R���}���܂Ƃ߂Ăǂ����ɃV���ƂȂ��ďo�����A�Q�S�Z���g�̋������E���t�i�M�^�[�̃E���t��g�[���Ƃ͈قȂ�A���a���Ȃ������̋����̂��ƂŁA�����ł͖�1/4�����̍��j�̕s���ȉ����ƂȂ��Ă��܂����ƂɂȂ�܂��B
�͉̂��y��ł̘a���̋Z�@�����B���Ă��܂���ł������A�]�����s���Ȃ��������Ƃ���A�\���g�p�ɑς����鉹���������̂ł��B����͐F�X�ȉ����̒��ł������ɗǂ��ł������̂ł�������A���̌���L���n��ʼni���g��ꂽ��ł��B���ɒP�����Ŏg�p����A���������炩�Ȑ�����t�ł邱�Ƃ��ł��鉹���ł����B�O���S���I���̂�����l�ɂƂ��Ă��A�S��������������Ă��邱�Ƃ͓��M���ׂ����Ƃł��B���{�̉������ǂ̂悤�ɂł����̂��A�܂��`����ꂽ�̂�������܂��A����ȑO������Ƀs�^�S���X�������g���Ă����ƍl�����܂��B���Ƀs�^�S���X���K�̃Z���g�l��\�Q�Ɏ����܂��B
�\�Q�@�s�^�S���X�����̃Z���g�l

�s�^�S���X���������ƂȂ��������́A��͂�~�̉��ł����B�������Ƃ̈Ⴂ�͂Q�Q�Z���g�i���m�ɂ͂Q�P�D�T�Z���g�j������܂����A������V���g�j�b�N�E�R���}�ƌĂ�ł��܂��B���̃E���t�����ɂȂ����o�܂́A�����̃L���X�g���̋���Ŕ��B�����a���ւ̖ڊo�߂ł��B����ł̓O���S���I���̂��̂��F�肪�������Ă��܂������A�c�����Ԃ��������ߋ��a���鉹�Ƃ��Ȃ����̉����W����������A���a�������̔����������ߘa���@�����W���܂����B
����ɏ]���A����܂ł͗]����ɂȂ�Ȃ������E���t�̑��݂��s���������炷���ЂƂȂ����̂ł����B�R�x�������s���a�����������̂͂��̂悤�ȗ��R����ł��B
���S�ȉ����͂W�x�ƂT�x�A�S�x�����ŁA�܂�Q�{���ƂR�{�����������a���Ƃ��čl�����Ă��܂����B���݂ł������̉������u���S�v�Ƃ��������t��Y���ĕ\������̂͂��̂��߂ł��B
�������l���邱�Ƃ́A������{���Q�̒�����ǂ̂悤�ȍl�����Ŏ��p�ɂȂ���������̑g���������肷�邩�Ƃ������Ƃ�������ł��B���Ƃ��ƂT�{���͏����ȋ����ł�����A���݂͒m���Ă��܂������A�R�{���Ƃ̋������鉹�����\�����邱�Ƃ͂ł��܂���ł����B
�s�^�S���X�����͂T�{�����g�킸�A�{����̒����炻��ɋ߂������g���č\�����ꂽ�̂ł��B���̌��ʁA�a���@�̔��W�ƂƂ��ɕs�������鉹���ł��邱�Ƃ�������悤�ɂȂ����̂ł��B
�ܓx�����[�_�[�}�\
�����ŁA�����̒��ł��ꂼ��̉������ǂ��Ȃ��Ă��邩�}�ŕ\�����邱�Ƃɂ��܂��傤�B
�����̐���������ꍇ�́A��ʓI�ɂ͌ܓx�����~���ɒu���K�v�ȉ��ǂ������Ō��уZ���g�l���L�����@������܂����A�����f�l�ł��邽�߂����̕\�����@��������ɂ����Ǝv���̂ŁA���̓��[�_�[��`���[�g���g�����Ƃɂ��܂��B���̕��@�́u���̂����v�ł��镽�ϗ��̊e���Ƃ̉��������Z���g�l�ŕ\�킷���e�ŃO���t���쐬���܂��B�ܓx���̕\���͓����ł����AA����ɒ������邱�Ƃ��������Ƃ���A��0�Z���g�ɂ��čs�Ȃ��܂��BC���O�ɂ���������A��C�̃Z���g����S�Ẳ��ɉ�����ςނ��ƂŁA���݂̊W�͕ς�܂���A�����̐}�������g�喔�͏k�����邾���ł��B���l�ڐ��͉~�̒��S����f�[�^���e�ɂ��K�x�Ȕ͈́i-30�`30�j���O���̕����ɓ��S�~��ɐݒ肵�Ă��܂��B�����ɕ��ϗ���\������A���ϗ��Ƃ̔�r�ł�����S�Ă̐��l�͂O�ƂȂ�A�ڐ�0��ʉ߂���P�Q�p�`����`����邱�ƂɂȂ�܂��B
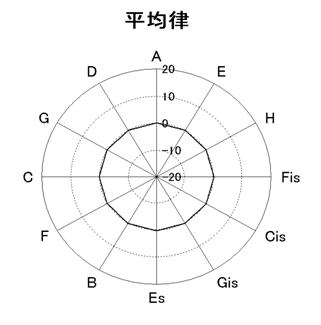
����ł͎��ۂɃO���t�ɂ��Ă݂܂��ƁA���ϗ��ƃs�^�S���X�����͐}�P�A�Q�̂悤�ɂȂ�܂��B
�}�P�@���ϗ��̌ܓx�����[�_�[�}
�@�@�@�@�@ 
�}�Q�@�s�^�S���X�����̌ܓx�����[�_�[�}
�@�@�@�@�@�@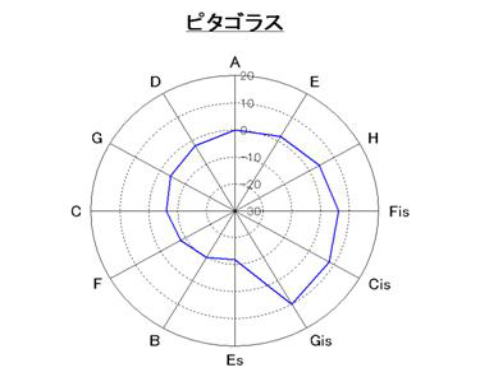
�s�^�S���X�����͌`�ɓ����������ĕ�����₷���ł��ˁB
���͂�����u�s�^�S���X�̊��L�v�ƌĂ�ł��܂��B�������A���ꂾ���ł͒P�ɉ����`�I�Ɍ��Ă��邾���ō\����������܂���A���̐}�Ɏ�v�ȉ����������Ĉꏏ�ɕ\�����܂��B
�O���t�̕\���͂S���ڂŁA�u�����v�Ƃ͑ΏۂƂȂ鉹���̊e���ƕ��ϗ��̊e���Ƃ̃Z���g���i�܂�Q�{���j�A�u�T�x�v�Ƃ͉����̊e���������Ƃ���T�x�����ƕ��ϗ��V�O�O�Z���g�Ƃ̃Z���g���i�܂�R�{���j�A���l�Ɂu���R�x�v�u�Z�R�x�v�Ƃ́A���̉��������Ƃ����Ƃ��̕��ϗ��S�O�O�i�T�{���j�A�R�O�O�Z���g�Ƃ̃Z���g�������[�_�[��O���t�ɂ�����@�ł��B�������邱�ƂŎ��o�I�ɂ��̘a���̓������m�F���邱�Ƃ��ł��܂��B���̗l�q���ēx�s�^�S���X�����Ō��Ă݂܂��傤�B
�}�R�@�s�^�S���X����
�@�@�@�@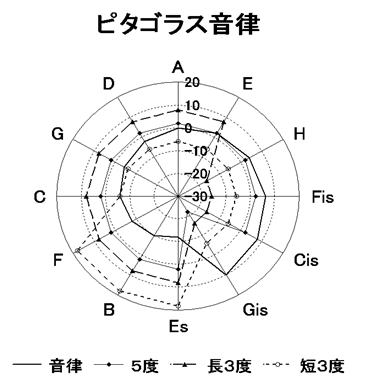
���̐}�̌����ł����A�܂�������\������������ƁA�ܓx�����ʼnE���ɂ��ǂ�ƂQ�Z���g�Â����Ă����܂��B���̐}������ƃs�^�S���X�����͎��v���ɊJ���Q����ɂȂ��Ă��邱�Ƃ�������܂��B�܂艹���Ƃ��Ă͂P�Q���Ŋ��������A�����Ɋg�����Ă��������ł��B
���������y�Ŏg�p�����ł̓I�N�^�[�u�������ɂ���K�v������܂��̂ŁA���̉���̒�����A�P�Q����1�I�N�^�[�u���o���Ďg�p���邱�ƂɂȂ�܂�����A��n�߂Ɛ�I���ł͂Q�Q�Z���g�̕����Ă��܂��܂��B���ꂪ�}��Es��Gis�̊Ԃ̗����Ƃ��ĕ\��Ă��܂��B�܂肱�̂T�x�������E���t���Ăяo���v���ƂȂ�܂��B
���ɂT�x�̍א�������ƁAEs����Cis�܂ł͂P�P��������+�Q�Z���g�ŘA�����A���ꂪ�s�^�S���X�����̗v�ƂȂ��Ă��܂��B�X�ɔj���̒��R�x������ƁAEs����E�܂ł̂W��+�W�Z���g�ŁA�����Ƃ̍����Q�Q�Z���g����܂��̂ŕs���ȋ����������܂����A��]����H����Gis�܂ł̂S��-�P�U�Z���g�ł�����A�����Ƃ̍����Q�Z���g�̔����������ƂȂ�܂��B
�Z�R�x�͒��R�x���d�˂�Ɗ��S�T�x�ɂȂ�A�����T�x��⊮����W�ɂ���܂��̂œ����悤�Ȍ��ۂ��Y���Č����܂��B�܂�j����C����Gis�܂ł̂X������AEs����F�܂ł̂R�������������܂��B
���̐����ł�������悤�ɁA���̐}�����鎞�ɕK�v�Ȃ��Ƃ́A���ꂼ��̉����Ŕ����������̂��ǂ������o���Ă������Ƃł��B����͏������̉��������ϗ��Ɣ�r���ĉ��Z���g�ɂȂ邩���o���Ă������Ƃł��B
�܂�A���S�T�x��+�Q�A���R�x��-�P�S�A�Z�R�x��+�P�U�Z���g�Ƃ������Ƃł��B
���蓾�Ȃ����Ƃł����A���z�̉���������Ƃ���A�}�S�̂悤�ɁA�R�}�������̂悤�ȓ��S�~��̏�ԂƂȂ�A�����͂O�ɁA�T�x��+�Q�A���R�x��-�P�S�ɁA�Z�R�x��+�P�U�ɕ`����邱�ƂɂȂ�܂��B
�}�S�@���z�̉���
�@�@�@�@�@�@�@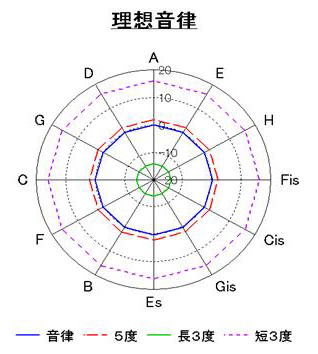
������o���Ă����������Ƃ́A���钲�ł̎�v�O�a�����l����ꍇ�́A���ׂ̏�����Ηǂ����ƂɂȂ�܂��B�Ⴆ�n�����ł͂T�x���G�ƂT�x����F�̊e���������邱�ƂɂȂ�܂��B���O�a���ł�Am��A�̒Z�R�x�ƂT�x�ŋ����̋���킩��܂��B�܂�ߐe���ł͓����悤�ȌX���������āA�ɂ₩�ɕω�������������̃o�����X�����čD�܂������ƂɂȂ�܂��B
�@
�Ƃ���ŁA���̃s�^�S���X�����̓�����a���I�ɍl���Ă݂܂��傤�B
�ʏ�͐F�X�Ȓ��ō�Ȃ��܂����A�y��ɂ����܂������t���Ղ��̂́A��͂�ω��L���̏��Ȃ������ł��ˁB�������ł͓]�����ł��܂���A���ɂ���Ē����������K�v������܂����A����Ȕς킵�����Ƃ͂Ȃ�ׂ��������Ȃ��ł�����A�E���t�̋��ق��������邽�߂ɁA�Ȃ�ׂ��������֒ǂ�����Ă����܂��B�n�����ł�Gis��Es�̊ԂłU�V�W�Z���g�ɂ��Ďg���܂��B
�Ƃ��낪�s�^�S���X�����ł́AEs����E�܂ł̕��i�悭�g�p���钲�ŁA�����̗ǂ��Ȃ����Z3�x���������Ă��Ďn���������̂ł��Bb��#���Q�A�R�t���Ă��钲�ł́A�قƂ�ǂ̒��Z�O�a���̋����������̂ł��B����ł͔��t�������Ȃ��Ȃ��Ă��܂��܂�����A���������̕����Y��ȉ������Ƃ������ƂɂȂ�܂��B
�@�Ƃ��낪�_�l�͎��X���Y������悤�ŁA���̉��������E���t���܂މ����̂Ƃ��ɏ����ƂQ�Z���g�������Ȃ��������������B���Ă����̂ł��B
H����Gis�܂ł̘a��������ɓ�����܂��B�}�Ō���ƈ�ڗđR�ł��B���ʂ͂��̂悤�Ȓ��͎g���܂����ˁB�ω��L�����U�A�V�t�������������������ɂȂ��Ă��邱�Ƃ��������ĉ��y������l�B�͋������悤�ł��B�̂̔��t�Ȃǂł͔��������Ă��������ȂǂƂ�������������悤�ł����A���������������������ƌ����Ă��A�M�^�[�ł͂�߂Ă���ƌ��������Ȃ�܂��ˁB�����������������������ɂȂ��āA���i�g�p����p�x�̍��������ŋ����̗ǂ��V���ȉ��������߂�悤�ɂȂ�܂����B
������
���݂̎��������{�l�́A���y�Ƃ����Ɛ��m�Ŕ��W�������̂̂悤�Ɏv�������ł������ۂ͂����ł͂Ȃ��A���̂悤�Ȓm�������^�����Ȃ������ɉ߂��܂���B���݂ł͈Ⴄ�̂ł��傤���A���̐���ł͉��y���̕ǂɈ̑�ȉ��y�Ƃ̎ʐ^���N�㏇�ɕ���ł��āA�o�b�n��w���f�������肩�特�y���n�܂����悤�ȋ�����܂������A����͊ԈႢ�������Ǝv���܂��B
���l�T���X��o���b�N���y�͖������W�I�ŕ����Ă��܂������A�Â����y�����邱�Ƃ͔��X�m���Ă��܂����̂ŁA���{�̉��y����͂ǂ��Ȃ��Ă����̂ł��傤���ˁB�Ƃ���ŁA���̃��l�T���X���Ɍ���ꂽ�̂��������ƒ��S�����Ƃ����V���������ł����B
�������ɂ��Ă͑��Â̐̂��猤������Ă�����ł����A�s�^�S���X���K�����𗘂����Ă������߁A���m�ł͂W�A�T�A�S�x�܂ł����a�����Ƃ��čl�����Ă����̂ł����ω��������Ă��܂��B�P���g�l�͋I���O���烈�[���b�p�̍L���n��ō����������ւ��Ă��܂������A���[�}�鍑�̑䓪�ƂƂ��ɃC�M���X��A�C�������h�ɒǂ�����Ă��܂��܂����B���̃P���g�l�̉��y�͏����R�x���g�����������Ô��ȓƓ��̋����������Ă��āA���O�̊ԂŎp����Ă��܂����B�A�C�������h��X�R�b�g�����h�ɔ��������w�������c����Ă��邱�Ƃł���������̂��ƂƎv���܂��B
���̉��y���P�S�`�P�T���I�ɂ����đ嗤�ɓ`�����A�l�[�f�������h�y�h��t�����h���y�h�ɑ傫�ȉe����^���܂����B����ɂ�菃���R�x��U�x�̕��s�ɂ��Ô��ȋ������x������A�����ȋ����Ƃ��ĉ����ɉ������邱�ƂɂȂ�܂��B�P�T���I�ɃX�y�C���̃o���C�g�����[�E�����X�Ƃ����l��5/4�̔䗦���܂މ�������܂����B�������A�s�^�S���X�������S�����������[���b�p�嗤�ł����ɂ͎�����܂���ł������A�P�U���I�ɂȂ��Ďx�������悤�ɂȂ�܂����B���ꂪ����R�Ɏ��������̂ł��B
�����ŏ��������ܓx�����[�_�[�Ő}�T�ɕ\�����Ă݂܂��傤�B
�}�T�@������
�@�@�@�@�@ 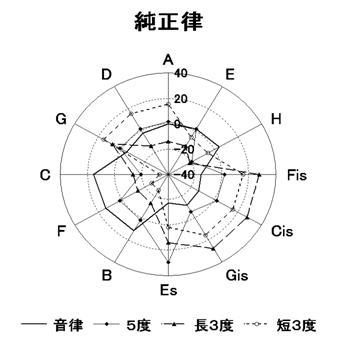
���̐}�ł́A����̑S���K�I���K�i�s�A�m�̔����̂݁j�ɉ����A�����ɑ������鉹�������Ă��܂��B�������AEs�ɂ��ẮA�����ł͐����̏����Ȕ䗦�ł���7/5���g�p���Ă��܂��B�V�{�����g��Ȃ����45/32���g���̂���ʓI�ł��傤�B�Ñ�M���V���ł�7�{�������ʂɎg���Ă����悤�ł��B�i�A���L���^�X�̓e�g���R�[�h������9/8�A8/7�A28/27�Ƃ����������g�p���Ă��܂��B�j
�@
���̐}�����āA�����L�̂悤�Ȍ`�������s�^�S���X�����̑��`�����A���҂����Y�^�Y�^�ɐ���悤�Ɋ�����͎̂������ł��傤���B
�Ɛl�͂T�{���̘A���ł��B�R�{���̔������Q�����o���o���ɒZ�����āA�f�^�����ɒ��荇�킳�ꂽ�悤�Ɍ����܂��B�t�Ƀ~�[���E�g�[���x���҂��炷��A�~�[���E�g�[���̔������L�k���Y�^�Y�^�ɂ����̂͂R�{���̓z��ł͂Ȃ����Ɣ��_����ł��傤�B������_�l�̈��Y�����m��܂���B
���j�����Ă݂�ƁA�\���R�̉����ŃX�y�C���̃g���h���C�X��������D�܂������A�����ɂ̓A���u�̋���Ȑ}���ق�����A�Ñ�M���V���̕������c����Ă��܂����B���̒��Ƀv�g���}�C�I�X�̒������u�a���_�v������A�e�g���R�[�h�̕����䗦�������X�̏������Ɠ������Ƃ���������A�s�^�S���X�������B���̉����ł͂Ȃ����Ƃ����炩�ɂȂ�܂����B�e�g���R�[�h�Ƃ̓M���V�����y�̗��_���\��������̂ŁA�S�x���������ĂS�̉��������Ƃ������̂ŁA������Q�Ȃ��ʼn��K�Ƃ������̂��M���V�����@�ł��B
���m�̉��y���_�͂��Ƃ��ƃM���V���̃e�g���R�[�h���_�����m�ɓ`�����A
�O���S���I���@�Ƃ��đ��݂��Ă��܂������A�Ǝ��̕ω��������Č��݂̒����ƒZ���̉��K�Ɏ������܂��B���݂̉��K�́A�u�h���~�t�@�v�Ɓu�\���V�h�v�̂Q�̃e�g���R�[�h���s�A���ɂȂ��������̂��ƍl���邱�Ƃ��ł��܂��B���@�ɂ��Ă͂����ł͐G��܂���̂ŁA��������l�͐�发�������o�Ă��܂����炻��������Ē��������Ǝv���܂��B
�@
���@�Ƃ��Ă̓����͘a���I�ȉ��y�Ɉڍs����ɂ�āA�ڒ���]���̌`�Œ��Z�����K�Ɏ�荞�܂�Ă����܂��B�������ł͂��̒��ł̂��ꂼ��̘a���͔��������̂ł������A��肪����܂����B����͑�S���Ə��S�������邱�ƂŁA���̂��ߓ]������Ɖ������̈ʒu���Y���܂��̂ŁA�����������Ȃ��Ȃ��Ă��܂��܂��B�Έʖ@�ɂ��Z�@���i�ނɂ�āA�|���t�H�j�[�ɂ��a�����d�v�������Ɏ���A�������ł͑Ή��ł��Ȃ��Ȃ��Ă����܂����B
���S�����i�~�[���E�g�[���j
������������w�i�̒��ŁA�~�[���E�g�[���Ƃ�������I�ȉ������P�T�Q�R�N�Ƀs�G�g���E�A�[�����ɂ���Ē���܂����B�s�^�S���X�����������T�x����ɍ\������Ă���̂ɑ��A�����R�x����ɉ������\�����锭�z�����܂ꂽ�̂ł��B���̉����́A�s�^�S���X�����Ō����Ă����R�x�����������ɂ���Ƃ�������������܂��B�܂��ނ���~�܂ł̂Q�Q�Z���g�̌덷�ł���V���g�j�b�N�E�R���}�i����͂S��̊��S�T�x�̐ςݏグ�ŏo�Ă���j��1/4�i5.5�Z���g�j�Âk�߂ď����ɂ��邱�Ƃł����B����ɂ��A�������ő�S���Ə��S��������s�s���������_����������A���̈ʒu���ނƃ~�̐^���ɂȂ�܂��̂ŁA���S�����ƌĂ�邱�ƂɂȂ�܂��B�u�~�[���E�g�[���v�Ƃ͂��̂悤�ȈӖ��ł��B
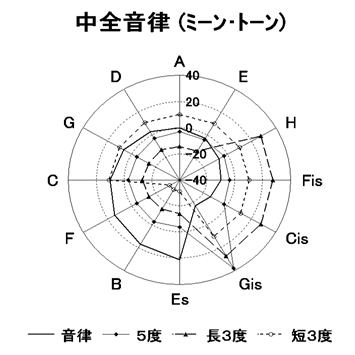
���S������}�U�ɏo���܂��傤�B
���ɖʔ����Ǝv���܂��B�s�^�S���X�����ƑΏ̂ɂȂ��Ă����ł��B
���x�͍����ɊJ���Ă��������L�ł��B�s�^�S���X�L�𗠕Ԃ��Č����̂Ɠ����ł��B���̐}���悭����Ƃ��̎����悭�킩��܂��B�E���t�̈ʒu�͓����ł����A�s�^�S���X�ł�Gis�ł̂T�x��������-�Q�Q�Z���g�ł������A���x�͂R�W�Z���g������܂��B
���Z�R�x�̔����������i�g�p���钲���Ő��܂��悤�ɂȂ�܂����B�s�^�S���X�����Ƃ͑S���t�ɂȂ����̂ł��B�������A�T�x�̉����͏����k�߂������������������Ȃ��Ă��܂����A���ۂɎO�a���Ƃ��Ēe���Ă݂�ƁA�s�^�S���X�������������������ƂȂ����̂ł����B
�}�U�@���S�����i�~�[���E�g�[���j
�@�@�@�@�@
���̉����͔�r�I�ȒP�ɒ����ł��܂����̂ŁA�`�F���o���Ȃǂ̌��Պy��Ɏg�p����A�o���b�N�̎���ɑ����̍�ȉƂ���x������܂����B
�w���f���͂��̉������D��ł��܂������A���[�c�@���g�����̉����œ]���\�Ȓ�����I��ł����悤�ł��B���m�ł͂��Ȃ蒷���Ԃ��̉�����������l�B�������悤�ŁA���ϗ����S���ɂȂ����Ƃ��ɁA�}�[���[�̓~�[���E�g�[�����Ȃ��Ȃ������Ƃ�Q�����Ƃ����b������܂��B
�w���f���̃~�[���E�g�[���D���͂��Ȃ�Ȃ悤�ŁA�]���̋��������������邽�߁A�E���t�����܂�o�Ȃ��悤�ɍl�Ă��ꂽ�u�������v�i�X�u�Z�~�g�j�E���j����������A�g�p���������ł��B����͂ǂ����������Ƃ����ƁA���܂Řb��ɂ��Ă��������Ƃ����̂́A���ϗ��������āu�J���������v�Ƃ������ʓ_�����������̂ł��B�܂艹��Ƃ��ẮA�f���{���ɂ�鏃���ȋ�������Ղɋ��߂Ă������߁A�I�N�^�[�u���z����Ƃǂ�ǂ��J���č��v���鎖���Ȃ������̂ł��B�I�N�^�[�u���g���Ȃ����K�ȂǑz�����邾���ł����|�ł��ˁB��̉���p�ӂ����Ȃ�Ή��y�����H�ł���̂��r���ɕ��܂��B�ł�������ۂ͔{����̒����畨���I�ɂP�I�N�^�[�u�����A�Q�{���Ƃ��ẴI�N�^�[�u���d�˂Ďg�p���Ă��������Ȃ̂ł��B���ϗ��̂悤�ɂP�Q���Ŋ������A�I�N�^�[�u�㉺���Ă������I�ɓ����ɂȂ�A�A�����ĂȂ��邱�Ƃ��Ȃ������������̂ł��B
�@��������������₷�������Ɓu�ٖ��ى��v�̉����������Ƃ������Ƃł��B
�Ⴆ�AD#��Eb�͕��ϗ��ł͓������ł����A�����͈Ⴄ���Ƃ��čl�����Ă��܂����B����͍��ł��������ƂȂ̂ł����A���ݎg�p���Ă��鉹�����������i�ٖ��������G���E�n�[���j�b�N�j�ɂȂ��Ă���̂ŁA���i�͍l���邱�Ƃ��Ȃ��Ȃ��Ă��邾���ł��B���̂��Ƃ���A����������#��b���ĕʁX�̉��Ƃ������Պy�킪����A�w���f���͎g�p�������Ƃ��m���Ă��܂��B
�@
���́A�M�^�[�ɂ��~�[���E�g�[�������̂��̂����݂��܂��B��������ƃA�b�Ƌ��������܂������A�|�������苻��������ł������Ȃ��̂ł��傤���B�t���b�g�������ɑŐ݂��ꂸ�ɁA��Ď������Ă��镔��������܂��B����͖{���ɒe����̂��ƍl���Ă��܂������ȕ|��������܂��B���͂��̊y��������Ō������Ƃ͂���܂��A�~�[���E�g�[���̎������͂��̂܂܂ł�����A�E���t���]���̕s�s�������������̂ł��邱�Ƃɂ͕ς肠��܂���B
�������A�����H�v����t���b�g���ɑŐ݂��A�������ɑ������镪���t���b�g�E�M�^�[�삷����@������܂��B���܂łɍ���ė����~�[���E�g�[���M�^�[�͂������Ē����ɑł��ꂽ�t���b�g�ɁA���i�g�p����p�x�̍����ω����������lj����č���Ă��܂��B���݂ł�������x�̎g�p�ɑς���ɂ́A���������������Ȃ��Ɠ���ł��낤�Ǝ��͍l���A��葽���lj������w�̐v�}�����͍���Ă݂܂����̂ŁA��ŏЉ�悤�Ǝv���܂��B
�@
�b�����ɖ߂��āA�s�^�S���X���������������ٖ��ى��̉����ł̓I�N�^�[�u�̒��ɑ�R�̉���p�ӂ��Ȃ���Ȃ�Ȃ������ł��邱�ƂɂȂ�܂��B
���������ۂɂ͖����̉���p�ӂł��܂���A�������͐l����������������x�̊J�������������A�@���ɂ��Č����ǂ��I�юg�p���邩�Ƃ������ƌ����܂��B
�ٖ������̒��������i�E�F���E�e���y�������g�j
���̌�A����͘a���D�ʂ̕����ɐi��ł����܂����A�]�����鐧��������͉̂��y��n�������ł͔@���ɂ������ł�����A�w���f���Ƃ͑S���Ⴄ�l����������l��������̂ł��B���̑�\���o�b�n�ł����B
�o�b�n�̉��y���̂��Έʖ@����ՂƂ����l���ł��������߂��A�a���I�ȋ��������ɂƂ��ꂸ�A�����钲�ւ̓]�����\�Ȃ悤�ɉ������̂�K�x�ɒ������āu���������v�����A�ٖ������ŃE���t�����H�v���s�Ȃ��܂����B�����Đ��܂ꂽ��i���L���ȁu���ϗ��N�����B�[�A�ȏW�v�ł��B
���������̔��z�̓��F���N�}�C�X�^�[���P�U�X�P�A�P�U�X�V�A�P�V�O�V�N�ɘ_�����\���Ēm����悤�ɂȂ�܂����B
�E���t���Ȃ����S�Ă̒��ʼn��t�\�ȉ����ł��B���������������E�F���E�e���y�������g�Ƃ����܂����A�o�b�n�͓Ǝ��̒������s�Ȃ��Ă����悤�ł��B
�N�����B�[�A����K���鎞�͂P�O�`�P�T�����炢�Ŏ��炪�������ς܂����Ƃ������Ƃł�����A�����Ɋ��ꂽ��Ƃ������Ǝv���܂��B�e���y�������g�͉����̈Ӗ��ł�����A�ǂ��������ꂽ�������E�F���E�e���y�������g�ł��B
�o�b�n�̌���A��q�ł������L�����x���K�[�⃔�@���b�e�B�A�����O�A�P���i�[���A�ٖ������̕����u���������v���l�Ă���l�������܂����B
�@
�����͐F�X�Ȍ�����������炵���A���F���N�}�C�X�^�[�̒����ϗ��ł���ƍl���Ă�����A���������������ꂽ�ÓT������S�ĕ��ϗ��ł���ƍl���Ă���l�������悤�ł��B�{���̓������ϗ��͂��̎����ɂ̓����Z���k�����\���Ă����̂Ő����I�ɂ����ɒm���Ă��܂������A�M�^�[�ł͎g�p����Ă��܂����B
���ϗ�����ʂɕ��y�����̂̓s�A�m���s�̂����悤�ɂȂ����P�W�S�Q�N���炾�ƌ����Ă��܂��B���������b��͏��a�T�W�N�ɏo�ł��ꂽ�A�����B�i���́u�[���E�r�[�g�̍Ĕ����v�ȗ��A���{�ł��������i�݁A�����Â��Ԃ����炩�ɂȂ��Ă��܂����B���������Ă�����{�̉��y���T�����̂�����̐����͊Ԉ���Ă���L�q�������悤�ł��B
�Ƃ���ŁA���̃E�F���E�e���y�������g�̓����͒��ɂ���ĐF�ʊ����قȂ�Ƃ������ƂŁA�s�^�S���X�����ƃ~�[���E�g�[���̊Ԃ��ܓx������ď����ڍs���Ă����悤�ȁA�_�C�i�~�Y�������܂��Ƃ���Ă��܂��B�ł�����o�b�n�̕��ϗ��N�����B�[�A�ȏW��#��b�����Ȃ������͓����Řa���I�ȋ����������A������ɏ]���ċ����ɋْ����������Ă����A�����I�ȋ����Ɍ��������e�ɕω�����Ƃ������Ƃł��B
�����ȂƂ���A�M�^�[���������e���Ȃ����Ƃ��Ă͊W�Ȃ��Ǝv���Ă��܂������Ƃ���Ȃ̂ł����A��ǂ��ɂ��Ȃ�Ȃ����Ǝv�������Ƃ�����܂��B
����̓��R�[�_�[�����̔��\��Ŕ��t�����鎞�ł����B���R�[�_�[�Ɖ���������Ȃ����߁A�ŏ��̓��R�[�_�[�t�҂����ł͂Ȃ����特���������̂��Ǝv���Ă����̂ł����A�`�F���o���̒��������Ă���l�ɉ����͉����ƕ������Ƃ���A���@���b�e�B�ł��Ƃ̕Ԏ��������̂ł��B
����ł͍����킯���Ȃ��ł��ˁB�܂��l���Ă݂�Ε��ϗ��̃M�^�[�ɋ߂��������ƌ����Ȃ����Ȃ��ł����AA�Ń��R�[�_�[�ɍ��킹��ƁA���炩�ɃM�^�[���S�̓I�ɒ�߂ɂȂ�܂��B����͌ܓx�����[�_�[�}������悭������܂��B�Ⴆ�A���@���b�e�B�����̃��R�[�_�[��A�̉��ŃM�^�[�������Ƃ��܂��ƁA���@���b�e�B�����ł͌ܓx��������D����Gis�܂ł̂V�����ϗ��̂O��荂���ACis�������ŁA�Ⴂ���̂�E�AH�AFis�̂R�����ł����A���̘a���͉��t�p�x���Ⴂ�̂ł��B
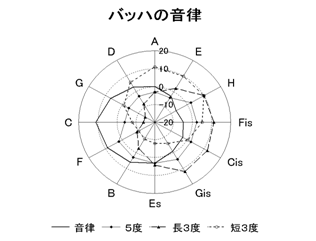
����ł͂����Ŋ���̃E�F���E�e���y�������g������\�����܂��̂Ŋm�F���Ă݂Ă��������B
�@�@�@�@�@�@�@�@�@�@�}�V
�@�@�@�@�@�@�@
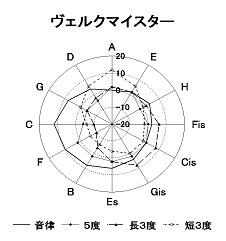
�@�@�@�@�@�@�@�@�@�@�}�W
�@�@�@�@�@�@�@�@
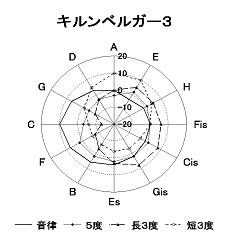
�@�@�@�@�@�@�@�@�@�}�X
�@�@�@�@�@�@�@�@�@�@�@
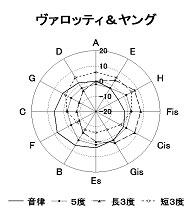
�@�@�@�@�@�@�@�@�@�@�}�P�O
�@�@�@�@�@�@�@�@�@�@
�@�@�@�@�@�@�@�@�@�}�P�P
�@�@�@�@�@�@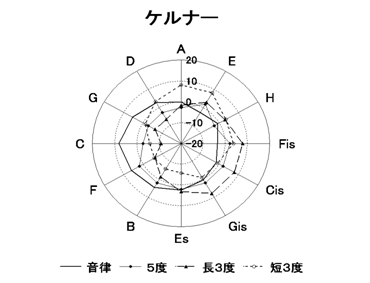
���̂悤�ȉ����̃M�^�[�����Ȃ��͂Ȃ��ł����A�����Ⴎ����ȃt���b�g�ł���������J���邾�낤�Ǝv���܂��B����ȑO�ɂ���ȃM�^�[�삵�Ă����l�͖w�ǂ��Ȃ��̂ł͂Ȃ����Ǝv���܂��B
���ꂼ��ɑ����̈Ⴂ�͂�����̂́A�T�ˎ����悤�Ȋ��������܂��B���ꂼ��̉����͌`���~�ɋ߂��Ȃ邱�ƂŁA�אڂ���a���Ƌ����̕ω������炩�ɂȂ�A�O�ɋ߂Â����Ƃŕ��ϗ��ɋ߂��Ȃ�܂��B���ꂼ��̉~�͂��̉����Ŕ����������G���A��ʉ߂��A�����̏����x�̈Ⴂ�ɂ��c�ݕ����قȂ��Ă��܂��B
�M�^�[�ւ̉����m���̉��p�i�����j
�������������̘b�����Ă��܂�����A�����ׂɂȂ�b���������̂ł����A�v���t�����Ƃ͒����̕��@��������܂���B�������A����͋��ɂ̒����@�Ƃ����Ă����������m��܂���B�����d�q�`���[�i�[���g���܂����A����͊A�����킹�鎞�₤�邳���ꏊ�Œ������Ȃ���Ȃ�Ȃ����Ƃ��A����ꂽ�ړI�Ɨp�r�Ŏg���܂��B�����ă`���[�i�[�̒ʂ�ɂ͂��܂���B�ŋ߂̖ڐ���̕t���Ă��Ȃ��@��ł͂ǂ̂��炢�������̂��Z���g�l��������܂���̂ł����������͎̂g���܂���B
�����Ɍ����܂��ƁA���ɂ͐������C�ɓ������悤�ɒ����o���Ȃ�����ł��B
���炩�Ɏ��Œ�����������S�n�ǂ��Ȃ�܂��B�܂��ŏ��ɒ����Ƃ͂ǂ�Ȃ��Ƃ�����̂��Ƃ������Ƃł��B�n���ɂ���ȂƎv����������邩������܂��A�ӊO�ƍl���Ⴂ�����Ă���̂ł͂Ȃ����Ǝv���܂��B�����������悤�Ɋe����K���ȉ����ɍ��킹�邱�Ƃł����A���̔�������������Ƃ����Ƃ���̈Ӗ��������Ⴄ�̂ł͂Ȃ����Ǝv���܂��B�����Ƃ͉����̂Ƃ���Ɋe���̉����߂��邱�Ƃł��B�܂�A�������������Ɓ������ɋ����悤�ɒ�������Ƃ������Ƃł͂���܂���B
��̓I�Ɍ����܂��ƁA���ϗ��ɏ]���Ċe���̊J���������邱�Ƃł��B
�M�^�[�͊�{���S�x�����ł�����A�����̋����Ƃ͂Q�Z���g�̍�������܂��B�Ⴂ��������Ȃ��悤�Ȃ��̋͂��ȉ��������炱���A�����ɍ��킹�邱�ƂƊ��Ⴂ���A���͒�����i�߂邤���ɍ����ǂ�ǂ�傫���Ȃ��Ă����܂��B
�Ⴂ��������Ȃ���������������ɒ�������Ǝv���Ă��܂������ł����A���ꂪ�����ōs�Ȃ��Ӗ������Ⴂ���鍪���ƂȂ��Ă���̂ł��B
�����������ȋ����Œ�������Ƃǂ��Ȃ邩���l���Ă݂܂��傤�B
�܂��D������ɂV�t���b�g�̃n�[���j�b�N�X�Ń~�̉����o���܂��ƁA�����̂T�x�����ł�����{�Q�Z���g�̍����ɂȂ�܂��B
���̉��Ɠ��������ɇE���̂T�t���b�g�̃n�[���j�b�N�X�����킹�܂�����A�E���̊J�����͂��̂Q�I�N�^�[�u�Ⴂ�~�ƂȂ�A�{�Q�Z���g������������܂��B
���l�ɇ@�����~�Œ�������Γ������ʂƂȂ�܂��B
���ɇC���Ɉڂ�܂����A���x�͇D���̂T�t���b�g�̃n�[���j�b�N�X�͊��S�ȂQ�I�N�^�[�u�ł����炢���̂ł����A�V�t���b�g�͊J���������{�Q�Z���g�����̂ł�����A�C���̊J�����͇E���Ƃ͋t�Ɂ|�Q�Z���g�̍����Œ�������邱�ƂɂȂ�܂��B
���l�ɇB���ƇC�����n�[���j�b�N�X�ō��킹�܂��ƁA�X�Ɂ|�Q�Z���g�Ⴍ�Ȃ�|�S�Z���g�ɂȂ�܂��B
�c��͇A���ł����A����͂������l�ɂ���ĈقȂ�ł��傤���A�Ⴆ�·E���̂V�t���b�g�̃n�[���j�b�N�X���V�ł�����A����ɍ��킹�܂��ƇE�������Ɂ{�Q�Z���g�ł�����A�V�̉��́{�S�Z���g�ɂȂ�܂��B
���̌��ʁA�B���̃\�ƇA���̃V�͂W�Z���g�̊J�����o���܂��B
���X���ϗ��̒��R�x�͏����ɑ��ā{�P�S�Z���g�������̂ł�����A���v�Ł{�Q�Q�Z���g�̉����W�ɂȂ��Ă��܂��܂��B����͂f�̘a���ł���s�^�S���X�����̒��R�x�Ɠ����ł��B�������Ȃ�悤�ɂƂ������荇�킹���͂��Ȃ̂ɁA����ꂽ�s�^�S���X�R�x�Ɠ��������ɂȂ��Ă��܂�����ł��B
���̌��ʂ́A�����������悤�ɍ��킹��Ƃ����Ӗ������Ⴂ���Ă��邱�Ƃɂ����̂ł��B
�`���[�i�[���g�����̉����͕��ϗ��̂O�ł�����A�������͂Ȃ��Ƃ����Ă��䖝���o������x�ł��B
���̗�ł�������̂悤�ɁA�����Ƃ͎g���Ă��鉹���̂Ƃ���ɉ��������킹�邱�Ƃł��邱�Ƃ𗝉����Ȃ���Ȃ�܂���B
�����`���[�i�[�ʂ�ɂ��Ȃ��ƌ����܂������A����͕��ϗ��������Ăł���������A�����̈Ⴂ�ݏo���ē���̏ꏊ�ŋ�����ǂ��������Ǝv���Ă��邱�Ƃɂق��Ȃ�܂���B���������̃M�^�[�t�҂͂����������Ƃʂɍs�Ȃ��Ă�����̂Ǝv���܂��B�����Ɏ��M�̂���l�͈����������Ă݂�̂�������������܂���ˁB
�@���ϗ��̒��������鎞�ɁA�d�q�`���[�i�[���Ȃ��������̃s�A�m�����t��
�ǂ����Ă������Ƃ����ƁA�̂���̕��@�Łu���Ȃ�v�𐔂��Ă����Ƃ������Ƃł��B�����1�b�ԂɂS�`�T��́u���Ȃ�v�ƂȂ�悤�ɒ�������Ƃ������̂ł��B
�����M�^�[�̒����Ō��݂͂��̕��@���g�p���Ă��܂��B
���̕��@�͍ŏI�`�F�b�N�Ɏg���܂����A�܂��n�߂ɒʏ�ʂ�ɇD���̊J��������ɇE�C�@�ƊJ�����ō��킹�A���ɇE����A���A�C����B���J�����ō��킹�܂��B���ꂩ��אڌ��Ƃ̋���T�A�S�t���b�g�ʼn������Ċm�F���A�~�̉����e���Ŋm�F���Ă���A�Ō�ɇD���̊J����A�Ƃ��̑��̊e����Cis�̒��R�x�́u���Ȃ�v�𐔂��܂��B
�A�B�C���ł͓��������ł�����P�O�x�̉����i�I�N�^�[�u+���R�x�j�́u���Ȃ�v���A������������ɂȂ�悤�ɒ������܂��B���̌�͇@���ƇE���̂X�t���b�g��Cis�ŁA�����悤�Ɂu���Ȃ�v���������ɂȂ�悤�������ďI���܂��B
�܂�A�D������ɑ��̑S�Ă̌��ł�Cis�̉����Ő�����u���Ȃ�v�ꂷ�邱�Ƃł��B�M�^�[�̒����ň�ԓ���Ɗ�����͇̂A�B�C���̃o�����X�ł�����A���Œ�������ꍇ�̈�Ԋm���ȕ��@�ł���A����ȏ�̃`�F�b�N���@�͖����̂ł͂Ȃ����Ǝv���Ă��܂��B
�@
���ʂ́u���Ȃ�v�̂Ȃ��[���E�r�[�g�ō��킹��̂���ʓI�ł����A�����v���ɁA���j�]����I�N�^�[�u�ł͋��e�͈͂��L�߂��ă|�C���g�f����̂�����悤�Ɏv���܂��B
�܂�A�u���Ȃ�v�̏o�Ȃ����������Ȃ�L���Ɗ����Ă��܂��B��������͉�X�̊��o���E���炭����̂ł͂Ȃ����Ǝv���܂����A�T�`�U�Z���g�ʂ̕��������Ă��܂��B����Ɉ��������R�x�Ń`�F�b�N���鎞�ɂ́A���炩���߂قڐ��K�ȏ�Ԃɒ�������Ă��邽�߁A���ϗ��́u���Ȃ�v���m�F�ł��܂��̂ŁA�u���Ȃ�v�̉ł��̌����������Ⴂ����������܂����A���������ł͋͂��ȁu���Ȃ�v�ł͍����̂��Ⴂ�̂����f���邱�Ƃ�����Ǝv���܂��B
���̕��@�ł��ƁA�����̉����ω��ł��u���Ȃ�v�̐����ς�܂�����A��������
�A�\�r�����Ȃ���Ίy�ɏC���ł��܂��B�ň��ł��u���Ȃ�v�̐������낦�Ă����·D���������Y���Ă��邾���ɂȂ�܂�����A���̕��@�����ɂ��ƍl���鍪���ł��B
�@
���̑O�Ƀt���b�g�⌷�̐��x�A�����Z�p�̖�������܂����A�������̐��\���e�����傫���Ǝv���܂����A�אڌ��̋͂��ȉ����̈Ⴂ�ł��e�����o�����X�悭���ϗ��ɋ߂Â��邱�Ƃ������̋Ɉӂł���ƍl���Ă��܂��B���̂��Ƃ͒����ɂ��Y�����e�|�W�V�����łǂ̂悤�ɕω����邩�p�\�R�����g���ăV�~�����[�g���Ă݂�Ƃ悭������܂��B
���݂͊y��ƌ��̐��x�����Ȃ���サ�Ă��܂��̂ŁA���������ׂ��ȉ����̈Ⴂ�ɂ��q���ɔ������Ă���܂�����A
���������������邽�߂ɂ͑a���ɂ��Ȃ����Ƃ��厖�ł���Ǝv���܂��B
�e�퉹���ސ���
�������A�s�^�S���X�����A���S�����͊�{�I�ȍl�����Ƃ��Ĉٖ��ى��̉����ł��B���������̉��������H���悤�Ƃ���ƁA���_�l�̉���̒�����1�I�N�^�[�u��12�������A���̉��I�N�^�[�u�����d�˂ĉ��K�Ƃ��ĂȂ��Ŏg�p���邱�ƂɂȂ�܂��B�����܂ŏ������͋����̖ڕW�ł���A���̑��̉����͂��̏����ȋ����ɋ߂Â����Ɠw�͂������ʐ��܂ꂽ���̂ł��B
�����ɂ͂R�{���ƂT�{���̂��߂�����������A�s�^�S���X�͏����T�x�i702�Z���g�j�ň��̂T�x���������A�~�[���E�g�[���͏����R�x�i386�Z���g�j���̗p���A���R�x�̊Ԋu���ϓ��ɂ������߁A�T�x�����i696�Z���g�j�����ɂȂ��Ă��܂��B
���ϗ����ϓ��ł�����T�x�͓��R���i700�Z���g�j�ŁA�܂肱�̂R�̉����͂T�x�����̈Ⴂ�Ƃ����_�����œ����m�ɋ敪���邱�Ƃ��ł��܂��B
���͂����̉������u�T�x�藦�����v�Ə̂��Đ������Ă��܂��B ���ϗ��͂��̗��҂̊ԂɈʒu���܂����A�T�x�����ł̓s�^�S���X���ł��B�����ĕ��ϗ��͑S�Ă��ϓ��ɂ��ăI�N�^�[�u�����S�Ɉ�v����悤�ݒ肵�����߁A�P�I�N�^�[�u�Ŋ�������u�����ٖ������̉����v�ɂȂ�܂����B
�������A�s�^�S���X�����A���S�����Ǝ��R�{���̌��ۂ����̂܂܉��y�Ɏ�荞�����Ǝ��݂��u�J�����ٖ��ى��̉����v�́A�l�Ԃ������̉��𑀍삷�邱�Ƃ��ł��Ȃ��Ƃ��������̑O�ɁA������Ƃ��ďI�����邱�ƂɂȂ�܂��B
�@
����ɑւ���Đ��܂ꂽ���������F���N�}�C�X�^�[���n�߂Ƃ��钲�������ł����A�I�N�^�[�u�Ŋ�����������ٖ������̉����ł��B
�l���悤�ł͕��ϗ������������ƈʒu�Â��邱�Ƃ��o����Ǝv���܂��B
����������̓����Z���k��������ӎ����čl�Ă����Ƃ��������A���̕��@�����������̍l���������Ă����Ƃ����ׂ��ł��傤�B
�����Z���k�̓t���b�g�����y��ŗL���Ɏg�p�ł��鉹���Ƃ��āA�܂�t���b�g���ɑŐ݉\�ł�����@�Ƃ��Ĕ��\���������ł���̂ł���A���H���l������ł̕��@�_�ł���Ƃ����܂��B���������Ƃ͂܂��Ɏ��H��O��Ƃ��������Ƃ��Đ��܂ꂽ���̂ł��B
�@
�����Ŋe��̉����ސ������Ă݂܂��B
*���R�����i�J���������j�F�������A�s�^�S���X�����A���S����
*�T�x�藦�����F�s�^�S���X�����A���S�����A���ϗ��A��������
*���������i���������j�F���ϗ��A���F���N�}�C�X�^�[�A�o�b�n�A ���@���b�e�B�i�����O�j�A�L�����x���K�[�A
�P���i�[�A��
���H�Ƃ��Ă̓����@
���y�̌���ł͎��H���l���ċ�̓I�ȉ��K�����Ȃ���Ȃ�܂��炻�̕��@���K�v�ł��B�̂���s���Ă����̂������@�Ƃ������̂ŁA1�I�N�^�[�u�����������ɕ����������̂����̍Œ�P�ʂƂ��A���̒P�ʂ����{�����Ă��ꂼ��̉������\��������@�ł��B���̒P�ʂ��R���}�Ƃ����܂����A����͊��ɏq�ׂ��s�^�S���X�E�R���}��V���g�j�b�N�E�R���}�Ƃ͑S���Ⴂ�܂��B
�ߎ��@�ł͂���܂����A���̎�@�͍�鉹����5�x�����������Ɍ���Ȃ��ߎ������邱�Ƃ̂ł��铙�������̗p���邱�ƂŁA�ȒP�ɖ͋[�������ł��Ă��܂��܂��B�����ċ���悢���͂P�Q�A�P�X�A�R�P�A�S�R�A�T�R�A�T�T�Ȃǂł��B
��ԃV���v���Ȃ��̂��P�Q�����ŁA�܂茻�ݎg���Ă��镽�ϗ��ł���A�S�����ʂ��Ȃ������ȍ\���ł��B�F�X����܂����ʔ������ƂɁA���̓����@�ŏ������ɂ��Ȃ�߂���������邱�Ƃ��ł��A�����������Ƃ����܂��B
�R�P�����Œ��S�����i�����|1/4�R���}�j�A�T�R�����œ����������i�s�^�S���X�����������Ɋ܂܂��j�A�T�T�����ŏ������ƒ��S�����̒��ԂɂȂ�T�T�������i�����|1/6�R���}�j���\���ł��܂��B
���ϗ������y����܂ł̌ÓT���烍�}���h�̎����ɂ́A�T�T�������������l�C���W�߂Ďg��ꂽ�悤�ł��B���̓���������\�R�Ō��Ă݂܂��傤�B
�\�R�@��������
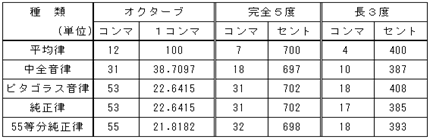
���l�ł͌f�o���܂��A���������ł���Ȃ�����A�{���̗��_�l�Ɣ�r���Ă݂Ă�1�Z���g�̌덷��������܂���A���ŕ����Ė{���Ƃ��̈Ⴂ�f���邱�Ƃ͂ł��Ȃ��Ǝv���܂��B
�@
���̂悤�ɁA�s�^�S���X�����͂T�x�̏��������Ƃ��āA�~�[���E�g�[���ł͂R�x�������Ƃ��邽�߂ɂT�x���U�Z���g�k�߂������Ƃ��āA���̗��ɂ̒��ɖ�Q�Z���g�Ԋu�ŕ��ϗ��ƂT�T�������������ʒu���邱�ƂɂȂ�܂��B
���̑��ɂ��ÓT�����̒��ɂ̓s�^�S���X�E�R���}����ɕ��U���邩�ňقȂ鉹�������݂��܂��B
�~�[���E�g�[���E�M�^�[�i�������d�l�j
�����������g�p���邱�ƂŁA�t�b���g���������y��̓t���b�g���ɑŐ݂��邱�Ƃ��ł��܂��B���̓T�^�����ϗ��ł���A�����Z���k���������̂ł��B�܂�A���������̓t���b�g���ɂ��邱�Ƃ��ł���Ƃ����Ӗ��ł��̂ŁA�����Ŏ����v�l�Ă����~�[���E�g�[���E�M�^�[���Љ�܂��傤�B
��̃~�[���E�g�[���̍��ڂł̓t���b�g���ꂽ���̂�����ƌ����܂������A�����@���g���~�[���E�g�[���̓t���b�g���ɐݒ肷�邱�Ƃ��ł��܂��B�����̊y�킪�������Ȃ��������R�́A�{���ٖ��ى��̉����ł���Ȃ���A���H��̓I�N�^�[�u�̏�����������Ƃ��ł��Ȃ����߁A1�I�N�^�[�u�����̉��������ۂɎg�p���Ȃ��������ɂ��܂��B
����͕������ł��������Ƃ������܂��B�g�U���鉹���̈ꕔ�������g���Ęa���I�ɂ��ǍD�ŁA�S�Ă̒��Ŏg���鉹�y����낤�Ƃ��邱�Ƃ��_���I�ɕs�\�ł��邱�Ƃ�m��Ȃ������̂ł��傤���B
���̓����͉Ȋw�I�ɉ��̌����������܂Ői��ł��Ȃ��������߁A�����I�ȗ����܂łɎ����Ă��Ȃ������̂�������܂���B���邢�́A�����Ă��Ȃ���������������ݏo�����������̂ł��傤���B
�@
���Ċy��̍\���ł����A���̃M�^�[��1�I�N�^�[�u�łP�Q�t���b�g�̃~�[���E�g�[���ł͂Ȃ��A�ٖ��ى����������镪�����i�X�u�Z�~�g�j�E���j��͂����M�^�[�ł��B�ނ̃w���f���������������~�[���E�g�[���ŁA�ٖ��ى����������悤�Ɛ��삳�ꂽ�������́A�������Ȃ萻�삳�ꂽ�悤�ł��B�������͊e�킠��悤�ł����A�P�X���̂��̂���ʓI�ł��傤�B�ł�����M�^�[�ł�����1�I�N�^�[�u�ɂP�X�t���b�g��Ő݂��邱�ƂɂȂ�܂��B
���Ƃ��ƃM�^�[�ł͑S�Ă̒���e�����Ƃ͂قƂ�ǂ���܂���̂ŁA���̃M�^�[�̐v�ł��ΏۂƂ��钲�́A�s�A�m�̔������Ɍ��肷����x�̐�����݂��Ă������̂ł͂Ȃ����Ǝv���܂��B�܂蒷���ł͌ܓx����F�`H�܂ł̂V���Ƃ��̕��s���ł���Z���V���ł��B
�NJy��̔��t�����鎞�Ȃǂ́A����1���Q��b�n��ɃV�t�g�������������̂�������܂��A��芸���������ł͔����̒���z�肵�悤�Ǝv���܂��B
�@
�����ɑ������镔�����Q�t���b�g�ɕ������܂�����A���t���鎞�ɂǂ����̃t���b�g�������邩�������ƂɂȂ�܂����A�����Ή��Ƃ��Ȃ�̂ł͂Ȃ����Ǝv���܂��B���̓Z�[�n���g���Ȃ��Ȃ鉟�����ł邱�Ƃł����A�������ł��邱�Ƃŏ����R�x���������悤�Ƃ���̂ł�����A�����̐���͊o�傷��K�v�����肻���ł��B
�@
���̃~�[���E�g�[���͂R�P���������ŋߎ�����������ł��B
���̈Ⴂ���ǂ̒��x���}�P�Q�Ō��Ă݂܂��傤�B
�}�P�Q�@�@�R�P�������S����
�@�@�@�@ �@�@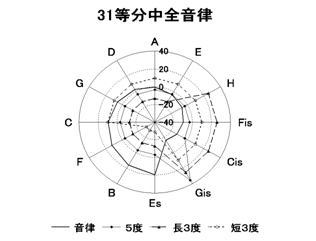
��U�}�Ɣ�r���Č��Ă��قƂ�Ǔ����ł��B���R�Ȃ̂����m��܂��A�_�l�͂���Ȑ�����p�ӂ��Ă����Ă��ꂽ�̂ł��ˁB�{���ɕs�v�c�ȋC�����܂��B�Ƃ���łR�P�������邱�ƂłP�X�t���b�g�ł�����P�Q�t���b�g���Ԉ������ƂɂȂ�܂��̂ŁA�ǂ���Ԉ������Ƃ�����肪����܂��B
�ΏۂƂ��钲�����l������ƁA�\�S�̂悤�ɂȂ�܂����B�]���ȉ����܂܂�Ă��܂����A�������Ȃ�ɑ����̒��Ŏg�p�ł��܂�����A�M�^�[�����̍�Ƃ��l���āA�t���b�g�͕��f���Ȃ��őS�ć@������E���܂łȂ������t���b�g�Ƃ��܂��B
���ʂ̃M�^�[�Ɣ�r����ƁA�t���b�g�Ԋu�������Ƃ���ł͖�1/3�ɂȂ邱�ƂɂȂ�܂����A�}���h�����̃n�C�|�W�V���������l����ƁA�M�^�[�ł����v�ł͂Ȃ����Ǝv���܂��B���̐U�����傫�����Ƃ��C�ɂȂ�܂����A�ʏ�̂P�Q�t���b�g�܂ł̎g�p�Ɍ��肵�Ďg�����Ƃ��l����A�g����̂ł͂Ȃ����Ǝv���܂��B�P�Q�t���b�g�ȏ�͊Ԋu�������Ȃ�܂��̂ŁA�g�p�p�x���Ⴂ���Ƃ�����A�����i�_�C�A�g�j�b�N�X�P�[���j�ɑ������鉹�݂̂��o��悤�ɂ���Ƃ����̂ł͂Ȃ����Ǝv���܂��B
���̃t���b�g�d�l��\�S�Ɏ����܂��B
�\�S�@�t���b�g�d�l�i���_�l�j
�@�@�@�@�@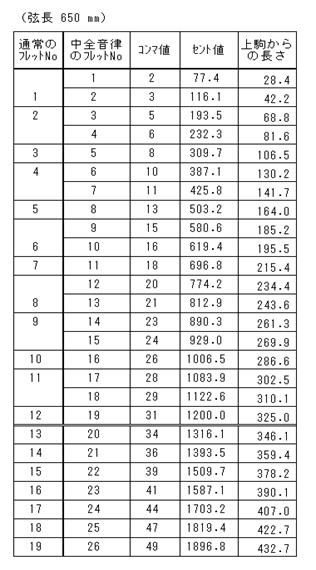
���̃M�^�[�����̓_�u���E�t���b�g�ƌĂ�ł��܂��B�������Ƃ����Ăѕ��ɍ��킹�ĕ����t���b�g�ƌ����Ă��Ӗ���������܂���ˁB
�@
��d�ɂ����t���b�g�́A�ʏ�ł͂ǂ���Ȃ̂��Ƃ������Ƃ��������߂ɁA�t���b�g�ԍ����㉺�ɏ��������Ă���܂��B�|�W�V�����}�[�N���|�W�V�����ɂ���Č`��ς��āA���߂ɕt���Ă����Ɨǂ��ł��傤�B�Ⴆ�Βʏ�̂V�t���b�g�́u���v�ŁA�R��T��P�O�t���b�g�́u���v�A�c��͒��_�u�E�v���������̂ł͂Ȃ����Ǝv���܂��B
�������̂悭�I�V���̐l���g���Ă����u�_�͂���v�̂悤�Ȋ����ɂȂ�܂��ˁB����������h�Ƃ������ƂŔ��܂�����������܂���ˁB
���邢�͐̂̃M�^�[�̂悤�Ɏw�ʂɃ}�[�N������悵�A����ƍl����Δ������͗l���f�U�C�����Ă�������������܂���B���̂悤�ɂ��ďo���オ�����t���b�g�E�{�[�h�̉��̔z�u��\�T�ɂ��܂����B
�\�T�@�t���b�g�E�{�[�h�̉���
�@�@�@�@�@�@�@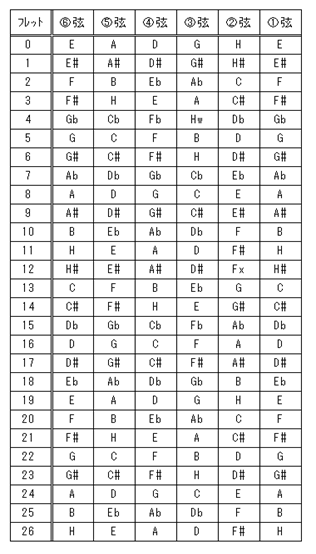
�������ꂽ�t���b�g�Œʏ�̃t���b�g�ɑ���������̂́A�@������E���܂ł̂����̂ǂꂩ�ɁA�K�������ɑ������鉹���܂܂�܂��B
�����āA�Ⴂ����#�ɑΉ�����������b�ɑΉ����܂��B�Ⴆ�A�@���̂Q�t���b�g��F#�͂R�t���b�g�ɂȂ�AGb�͂S�t���b�g�ɂȂ�܂��B
����͂T�x���������߂ɋN���邱�ƂŁA���ϗ��ł͈�v���ăG���E�n�[���j�b�N�ƂȂ�A�s�^�S���X�����ł�#��b�̈ʒu���t�ɂȂ�܂��̂ŁA������ʔ������ۂł��B���܂�g��Ȃ������Ǝv���A���̕����̃t���b�g���������Ă��܂��Ύg���₷�������m��܂��A�t���b�g��Ő݂���̂���ςɂȂ�܂����獢�������̂ł��B
�@
���̕\�̒���Fx�Ƃ�F�̃_�u���V���[�v�AHw�Ƃ�H�̃_�u���t���b�g�̂��Ƃł��B���̂悤�ɂ��Ĉٖ��ى��̉��y���Č��ł��邱�ƂɂȂ�܂��B
���̉������������w���f���̍�i�Ȃǂ�e���Ă݂������̂ł��B�Ƃ͌����A����͍\�z�̒i�K�̘b�ł�����A���̃M�^�[�����삳�ꂽ�Ƃ��Ă��A�ʂ����ĉ��t���\�������̊y���ő��v�Ȃ̂��A�S���C�t���Ă��Ȃ����肪�B��Ă��Ȃ��������Ă݂�K�v������܂��B�ނ���A���̂��Ƃ̕����y�퐻������[���ȓ�������Ă���\�������邩���m��܂���B
�ނ���y��Ƃ��Ă͍\���I�ȍH�v�̗]�n�͂���Ƃ��Ă��A�����Ƃ��Ă̓M�^�[�����؋Ղ�S�Ȃǂ̑Ŋy��̕��������Ă��邩������܂���B
���̑��̉����M�^�[
���̃~�[���E�g�[���E�M�^�[�����łȂ��A�T�T�������i���͂�����n�[�t�E�~�[���E�g�[���ƌĂ�ł��܂��j���g�p���āA�S�������v�̂ō�邱�Ƃ��ł��܂��B
�������A�t���b�g�Ԋu�������Ȃ邽�߁A�����⌷�̃r���t���Ȃǂ��C�ɂȂ�܂��̂ŁA�]���ȃt���b�g���폜������������ł͂Ȃ����Ǝv���Ă��܂��B
�t���b�g�����ɂȂ�̂Ȃ�A�������̂��ƒ��������ō�����ق������������m��܂���B
�n�[�t�E�~�[���E�g�[���ł̔������T�x�����ɖ߂������̂����@���b�e�B�ł��̂ŁA�����������ɂȂ���̂ƍl�����܂����A�t���b�g���P�Q�ŃG���E�n�[���j�b�N�ł��������݈Ղ������m��܂���B���R�[�_�[�̔��t�Ȃǂ����鎞�́A���̓J�����̉����ō���Ă��邩�l����K�v������ł��傤�B
���@���b�e�B�͌��݂ł������g���Ă��܂��̂ŁA������邱�Ƃ��ł���Ύ����Ă݂����Ǝv���܂��B���̑��ɂ����F���N�}�C�X�^�[��o�b�n���g���Ă����ł��낤���������l�ɍ���͂��ł��B
���������Ă݂͂����̂́A�Y������̐��t���b�g���w�ɕ���ł��Ă��A�����悭�e����Ƃ͎v���܂���̂ŁA�M�^�[�Ŏg�p���鉹���͊����̌ÓT���������̂܂ܗ��p���邱�Ƃ͓���ł��傤�B�M�^�[�̓������l��������ŁA�t���b�g�̃Y����a�炰��H�v������������V���ɍ쐬�����ق��������Ǝv���܂��B
���̍��Ŏ��ۂɎ����쐬�����������g���āA���ƃt���b�g��炸�ɋȂ��邱�ƂŁA������������������Љ�܂��傤�B
���̑O�ɁA�������̃M�^�[�ɂ��Č��y���Ă������Ǝv���܂����A����܂Ŋ���̎��݂��Ȃ���Ă���悤�ł����A���ɂ͏������̃M�^�[���ǂ����Ă��\�z���邱�Ƃ��ł��܂���ł����B
��{�I�ɖ����Ɋg�U���Ă����{�����L���̊y���Ƃ��Ď�荞�ނ��Ƃ͕s�\�ł�����A���H���邽�߂ɂ͐l�̊��o���x���l�������ߎ��@���g���čs�Ȃ������Ȃ��ł��傤�B�������߂T�R�����������ɂ��t���b�g���Ԉ����A����ꂽ�����ɑΉ�����{���̃_�u���E�t���b�g�Ɠ��l�ȕ��@�ŋ�̉����邩�A�����ƕʂ̉����ǂ��A�C�f�A���������薲����ł�������܂���B
�n���[�E�p�[�`�̃��m�t�H�j�[���_����̉�����悤�ȃA�C�f�A���M�^�[�ɓK���ł���A�ǂ�ȉ��y���o����̂ł��傤���B���邢�́A�����ȋ������g�������̉��y�́A����������Ɠd�q�y��ŃR���s���[�^���䂷�邵�����@���Ȃ��̂����m��Ȃ��Ǝv���Ă��܂��B
���������ɋ�藧�Ă����
���ϗ����S���̎���ɂ����āA�X�Ȃ鉹�������߂Â��铮�@�͂����������ł��傤���B���ϗ��͂S��N�ȏ���̉i�������̖��ɒH�蒅�������̂ł���A���ۂɕ��y���Ă��猻�݂܂ŕS�N���z���钷���ɓn���ċ��ɂ̉����Ƃ��Ďx������Ă��܂����B���ꂪ�����ɂ��āA�ǂ����ČÓT�����ɊS�����܂�̂��A�čl���Ă݂�̂��Ӗ��̂��邱�Ƃ�������܂���B
�@
���ϗ��ŕs�����c��v�f�Ƃ��ẮA�����I�ɂ͂R�x�����̑��肾���ł͂Ȃ����ƍl������̂ł����A���ϗ��ɔᔻ�I�Ȑl�͕ʂȌ����������邩������܂���B
�������������ϗ��ɂ��̍���D��ꂽ���ɁA�����Ȑl�X���猾��ꂽ���Ƃ́A�����ȋ����ƌ��ʂ�����ɁA�e���ɂ�����F�ʊ������������ꂽ�Ƃ������Ƃł����B�����������ɂ�鐫�i�̈Ⴂ�͒P�ɉ��������łȂ��A�����@����m���Ă̏ォ�m�炸���A�a���̑������ψ�ɂ��邱�Ƃ��ł����A���l�ɂ�������Ȃ������I�ȊW���琶�܂ꂽ���̂ł����B
�܂�A���̓����͍ŏ����狁�߂Ă������ƂƂ������́A�����ɋ߂��R�x��n��o�����ʂƂ��Ă̔���p�Ƃ��Ă����炳�ꂽ���̂ł����B�����ėǂ����������߂����ŁA���ϗ���������������܂ދ���������ɂ�������炸�A���̑���������p�����т���Ă��܂����B��������ۂ���l�Ǝ����l�Ƃł́A�@���Ȃ�l�����⊴�����̈Ⴂ������̂ł��傤���B
���j����{�Ɋт�����Ƃ��āA���������̋��������߂�v���������l�����̈Ⴂ���z���ĘA�ȂƗ���Ă�������ł������ƌ�����ł��傤�B
�������A�����܂Œ����N���������č����𑱂������R�́A�����ȋ����������ĉ������\������Ƃ������Ƃ��A�����I�Ȗ�������ł���Ƃ��ė�������Ă��Ȃ��������炱���A���p�̊ϓ_����ǂ̂悤�ɑI�����邩���A���������l�����̈Ⴄ�X�̔��f�ɂ䂾�˂��Ă��邱�Ƃɂ���̂ł͂Ȃ����ƍl�����܂��B
��̍l�����Ƃ��āA�����̑���ł����Ă���ɑ������Ƃɂ���āA����l�͊���ɂ���ĉ䖝���[�����邪�A�ʂ̐l�͕s�������~�ς��ĉ䖝�ł��Ȃ��Ȃ邱�Ƃ��l�����܂��B�����s���Ɗ�������x�͎��ۂɒ������Ȃ���킩��܂��A�������Ɋւ��Ă̂��̃{�[�_�[���C���͔����Ȉʒu�ɂ���悤�ȋC�����ĂȂ�܂���B�ނ���G���A���d�����Ă���O���C�]�[���Ȃ̂�������Ȃ��Ɗ����Ă��܂��B
�@
������l������v�f�Ƃ��āA����̒��x���Ⴄ���Ƃɂ��A��������̌�ł͏����̑��肪�������Ɗ����邱�Ƃ͍l�����܂��B�܂��r��p�̌��ʂł���A��l�łȂ����Ƃ��������ތ����ł���ƌ����Ȃ�������܂���B����Ƃ͑S���t�̊������Ƃ��āA����Ȃ�ɉ䖝�ł��鋿�����������ɁA���X�䖝�ł��Ȃ���������������������ׂɌ�����̂�������܂���B
�܂�A�����ɑ���l���ꂼ��̗v�����قȂ��Ă��邱�Ƃ������ł���悤�ɂ��v���܂��B
���͂��������v�����m���߂����āA���ۂɐ��삵�Ă݂悤�ƍl���܂����B����̐����₪�l�����܂����A�܂��͈�Ԍ����I�Ŏ��s�����Ȃ����̂�I�肵�悤�ƍl���܂����B
�_�u���E�t���b�g�͍\�������̃M�^�[�ƈႢ�߂���̂ŁA�C�t���Ȃ��������_���o�Ă���\�����������߃p�X���܂����B�����̌ÓT���������̂܂g���ƃt���b�g�����ɂȂ炴��܂���̂ŁA��������ɂ�������̂ł��B�����ŃM�^�[�����̐V���ȉ������v�ł��Ȃ����ƍl���܂����B
�M�^�[�Œ��������̎��� �@
�ŋ߂ł̓M�^�[�̐��E�ł��P�X���I�M�^�[���g����悤�ɂȂ�A�Êy��̍Č��������Ȃ��Ă��܂��̂ŁA���̕���ɂ����Ă͌ÓT���������H���Ă���l�X������悤�ł��B�������A�M�^�[�̓t���b�g�����y��ł��̂ŁA�����͕��ϗ����K���Ă���Ɨ�������ė��܂����̂ŁA����ȊO�̉����͗]��g���Ă���܂���ł����B
����ɉʊ��ɒ��킵���̂̓M�^�[�t�҂̐��_���M����ł����B���͂����g�ŊJ�����ꂽN-sys�Ƃ����t���b�e�B���O�E�V�X�e�����g���A�M�^�[����Ƃ̓c�����l���Ƃ̌����ŁA�t���b�g��炸�ɏ������Ȃ��邱�ƂŎ��p�����A���̃M�^�[���g���Ę^�����ꂽ�b�c����������Ă��܂��B
����͊e���̒���������ɕς���12�t���b�g�𒆐S�ɒ���A�i�b�g�ƃT�h�����M�U�M�U�ɂ��āA�t���b�g�̃Y�����ŏ����ɐݒ肷�邱�ƂŎ������Ă��܂��B
�@
���͂��̃V�X�e�����̗p�����A�i�b�g�ƃT�h���͏]���ʂ蒼���ɂ��āA�������̂��̂��M�^�[�ɍ��킹�ĕύX���邱�ƂŎ������悤�ƍl���܂����B��ʓI�ɂ͌ÓT�������g�p����ꍇ���A���炩�̉����̕ό`���Ă��܂��̂ŁA�V���ȉ������l���Ă��卷���Ȃ���ł��B���̂ق����y��̍\���ォ������̋����ɗ^����e�������炷���Ƃ��ł��A���肵���������ێ��ł���ƍl���܂����B
�@
�y��̐���́A���ɌÓT�y��̐���Ŏ��т̂���c�����l���Ɉ˗����A�����̂����d�オ��ƂȂ�܂����B�����ŁA�����̗p�����M�^�[�p�̒����������ǂ̂悤�Ȃ��̂����Љ��O�ɁA�����̐����𗝉������ŎQ�l�ɂȂ�ł��낤�ƍl���A���Ȃ�̉����j�̐����Ɖ��������̖ڕW�����Ă����܂��B
�����j�̑�_�ȗv��
�P�D�������͏����������W�߂������ʼn����Ԃ̑��݉������l�����Ȃ������̂Ŏ��s�����B
�Q�D�s�^�S���X�����͏����T�x�ł��������A�R�x�������������Ȃ������̂Ōh�����ꂽ�B
�R�D���S�����͏����R�x�ł��������A�T�x��������������͂Ȃ�����������ȃE���t������ł������ߑK�v�ł������B
�@
���������o�܂��玟��ɏ��������ɌŎ����Ȃ��ŁA���������ėl�X�Ȓ��ŗ��p�ł���悤�Ɋe��̉������o�ꂵ�����A�t���b�g�����M�^�[�ł̓����Z���k�̒������ϗ��ȊO�ɉ��p���邱�Ƃ�����ł������B
�@
���̎����܂�����ŁA�M�^�[�Œ����������������邽�߂ɂ́A�V���ȉ������\�z����K�v������A���̎����̂��߂Ɏ��̂悤�Ȑv�ڕW���f���Ď��g�ނ��Ƃɂ��܂����B
���������̖ڕW
�P�D���ϗ�����������������n��o���B���ɂR�x�����͏���(-14)�Ƃ̒���(-7)�����ǂ����������B
�Q�D�s�^�S���X�����̂R�x���������R�x�����Ȃ��B�܂�+�W�Z���g���傫���Ȃ�Ȃ����ƁB
�R�D���S�����̂T�x���������T�x�����Ȃ��B �܂�-3�Z���g��菬�����Ȃ�Ȃ����ƁB
�S�D�g�p�p�x�̍����a���ɔ�����������z�u����B �܂蔒���������Ƃ���a���i�_�C�A�g�j�b�N�̎O�a���j�ɔz�u����B
�T�D�������̕ω��͌ܓx���ɉ����Ċ��炩�ɕω�����悤�ɐݒ肷��B�������邱�ƂŁA���钲�����ŋ����̃o�����X���Ƃ邱�Ƃ��ł���B
�U�D�M�^�[�Ŏg�p�\�ȃt���b�g�̃Y����(�Smm����)�ƂȂ�悤�ɐݒ肷��B �@�ȏ�̖ڕW�����ׂĖ������鉹������肾�����ƂƂ��܂����B
���Ƃ��Ɨ��j��Œ������������܂ꂽ�w�i�́A�������ł̋�J���R�{���i�T�x�����j�ƂT�{���i�R�x�����j�̋������ڕW�ł������s�\�ł���A�T�x�̃s�^�S���X�����ƂR�x�̒��S�����̊Ԃ����炩�Ɉړ��ł���ܓx������邱�Ƃ��K�v�Ƃ��ꂽ�Ƃ������Ƃɂ���܂��B
�@
�l�����̈Ⴂ�ŐF�X�Ȃ��̂��ł������ł��ˁB�o�b�n�����ϗ��N�����B�[�A�ȏW�Ŏ��������@�͏����R�x���Q�̘a���Ŏ������Ă����悤�ł����A�s�^�S���X�����̂R�x���z������̂͂S����܂����B�M�^�[�ł̓t���b�g���Ȃ��Ǝ����ł��Ȃ������ł��ˁB�����R�x�ւ̂����������������܂��B
�@
���͂��̍�Ƃ����Ȃ���A���̂��̂悤�Ȃ��Ƃ�����̂����⎩�����A�����������\�z�����Ԃ̖ړI�́A����ꂽ�͈͂ł��������珃���ȋ����ɏ����ł��߂Â����Ƃ��ƌ��_�Â��܂����B
�����ăo�b�n�̉����͔[���̂������̂��Ǝv���܂������A�M�^�[�ł͍\����̐������珃���x�����x�ɂ�����܂��A���ϗ��ɂ���Đi����������̉��y�ɐ��������ƍl����Ȃ�A������x�̐��̒������J�o�[���Ȃ���Ύg�p�͈͂��啝�ɐ�������Ă��܂��܂��B�������Ċ��������M�^�[�p���������́A�s�^�S���X�����ƒ��S�����̂T�x�����̃Z���g�l�����x�ɂ��Čq�����n�C�u���b�h�ł���A���̂悤�ȉ����ƂȂ�܂����B
�}�P�R�@�M�^�[�p��������
�@�@�@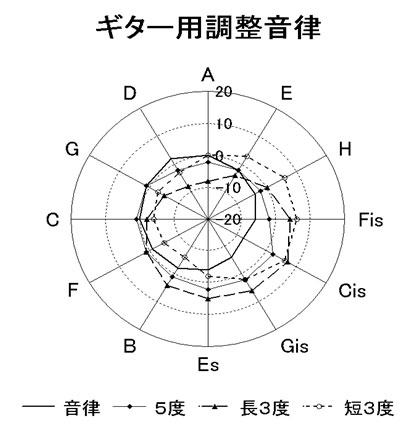
���̉����ł͂c�C�`���Y��ɏo��悤�ɂ��Ă��܂��B�f�̓M�^�[�̒�����̓s���ɂ��A�t���b�g�̋Ȃ�����������邽�߁A�����͏����ǂ��Ȃ���x�ɂ���K�v������܂��B�b�C�e�C�d���S�̂����܂��邽�߂ɁA�͂��ȉ��ǂɗ��߂���܂���ł����B
�\�U�@�M�^�[�p��������
�@ �@�@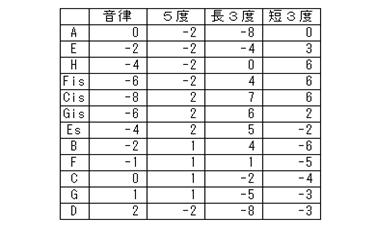
�ܓx���ɂ�����e���x�̍��v�����ꂼ��O�ɂȂ鎖�͊ȒP�ɏؖ��ł��܂����A�����I�ɂ��������邱�Ƃ��ł���ł��傤�B���R�x�����͂S�����ł����犄���āA
C+E+Gis = G+H+Es = D+Fis+B = A+F+Cis = �O �Ƃ����W�ɂȂ�܂����A�t���b�g�̃Y����4mm�������������邽�߂ɂ́A�T��Gis�R�x�|G�R�x���P�P����������Ȃ��ƃM�^�[�ł͏������N���A�[�ł��܂���B�X�ɁA�����̂Ȃ����炩�ȕω��Ƃ��邽�߂ɂ͂T�x�����̈��肪�K�v�ł����A�����𗐂��ő�̓G�͌��̐��x�ł�����A���̃����_���ȗ\���̂��Ȃ������h�~������@�̓M�N�V���N�������������Ȃ����ƂɂȂ�܂��B
�����������R����A���̒��x�̒���������Ȑ��ł��낤�ƍl���܂����B
���Պy��Ƃ͎���قȂ�A�ǂ����Ă����ϗ��ɋ߂��Ƃ���Ŏ��������邱�ƂɂȂ�A���ꂪ�M�^�[�̏h���Ȃ̂�������Ȃ��ƌ��܂����B
�@
�ЂƂ厖�Ȃ��Ƃ́A���̉������g�����ꍇ�͕ϒ����Ɍ����Ȃ����Ƃł��B
�`���[�j���O���Ⴄ�W�ŁA�E�����c�ɉ�����Ɖ����������܂��B���̈Ⴂ�́}�S�Z���g�ł����A����Ȃɂ���Ă͕s���ɂȂ邱�Ƃ��\������܂��B
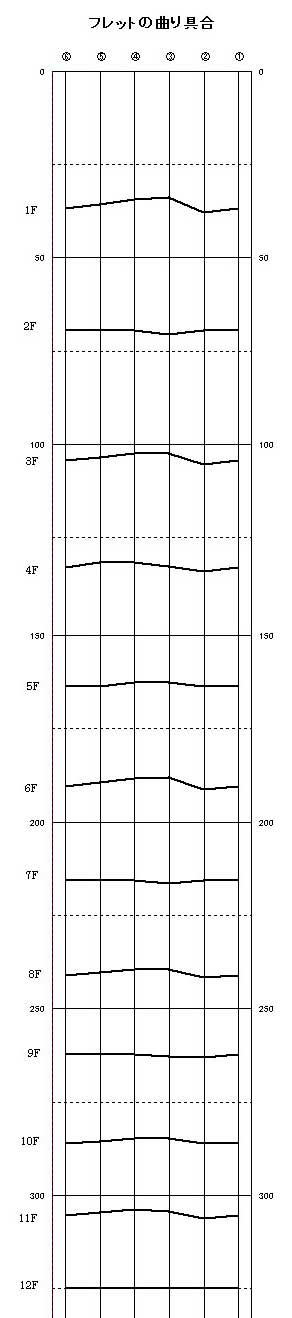
�����������邽�߂ɂ́A�i�|���I���E.�R�X�g�̂悤�ɂV���M�^�[�ɂ��āA
�F�����c�ɂ�����@���l�����܂��B���̐}�ŁA�t���b�g�̋Ȃ����悭�����ɂȂ��Ē��������Ǝv���܂��B��ԑ傫�ȋȂ�͑�P�t���b�g�ŁA�R�D�Xmm�ł����A�����������̋Ȃ�͋C�ɂȂ�Ȃ��Ȃ�Ǝv���܂��B
�}�P�S�@�t���b�g�̏�
�@�@�@�@�@ 
�����̗��j��H���Ă݂�ƁA�����̑����������������玟��ɔ��W���A�a���I�ɂ������I�ɂ����R�ɂȂꂽ���ϗ��܂ł̊ԂɁA���y���������ω����Ă��邱�ƂɋC�t���܂��B���[�c�@���g���x�[�g�[�x�����V���p�������ϗ��M�^�[�͒m���Ă��܂������A�ÓT�����s�A�m�����t���Ă��܂����B���ϗ���������������������Ƃ����Ă��A����������Ƃ����Ƃ�������邽�߁A��Ȃ����ł����������̂��Ƃ������Ă���悤�Ɏv���܂��B
�ł�����A���������������g�p����y��͂���Ȃ�̐���������Ȃ���Ȃ�Ȃ��Ƃ������Ƃł�����܂��B�����Ȃ�ŏ����痘�p���钲�͈̔͂��čl���A�Q�A�R��ނ̊y���p�ӂ�������̂��Ƃ��l���܂����A�o�ϓI�ȕ��S���傫���Ȃ�߂����肪�o�ė��܂��B�������čl���Ă݂�ƁA���ϗ��M�^�[�Ƃ������͖̂��ʂ��Ȃ����ɗǂ��ł������̂ł��邱�Ƃ������ł��܂��B����ł������͂����Ɨǂ��Ȃ�Ȃ����ƍl����̂͐l�Ԃ̐��Ȃ̂ł��傤�ˁB
�V���ȉ����̎�������
����A�V���ȉ����̃M�^�[�삷��O����A���ۂɃ��@���b�e�B�����Œ������ꂽ�`�F���o���̉��t�����x�������Ă��܂����̂ŁA�ÓT�����ŋ��������������̂����邱�Ƃ͏��m���Ă��܂����B�����ă��@���b�e�B�ȊO�̉������ǂ̂悤�Ȃ��̂��A�C���^�[�l�b�g�Œ���Ă��鎑�����`�F�b�N���Ă��܂����̂ŁA�ÓT���������������������Ă�������ł��B
�@
���̏�ł��̊y���e���Ă݂����z�́A�f���ɂ������ɐ\���܂��Ɓu���\�������Y�킾���A�z�����Ă������͑��肪���Ȃ��v�Ƃ������Ƃł����B���i�͎��B�����ϗ��Ɋ���Ă��邽�߂ɁA�����̐l�͂���قǍ����Ȃ��Ƃ�����ۂ����̂ł͂Ȃ����Ǝv���܂��B�ł����������l�̚n�D�Ɠ����ŁA���̋����͋C�ɓ���Ε��ϗ����g�������Ȃ��Ȃ邩���m��܂���B
�ǂ�������I�ׂΈ����������t���Ă��邱�Ƃ́A�����̐����ɂ���Ė����ł�����A���ɂƂ��Ă͑z�肵�Ă����͈͂ł����B�����Ď��̍l�Ă��������́A��{�I�Ƀ��@���b�e�B���������͂Ȃ�Ȃ����낤����ǁA����͌y�����邾�낤�Ɨ\�z���Ă������Ƃł�����A���̌��ʂ͔[�������Ă��܂��B
�@
���������ׂ����A�ڕW�Ƃ������ڂ��ǂ��Ȃ����̂������������Ǝv���܂��B
���̉����̑��̖ڕW�ł���������R�x�̋���������ꂽ���Ƃ����_�ɂ��ẮA����͗\��ʂ�̂��̂ƂȂ�܂����B�ǂ������̃��x���ϗ��Ə������̒��Ԃł���|�V�Z���g���������ɋ߂����Ƃ��K�{�ł���Ƃ��Đv���A�`�Ƃc�̂Q���|�W�ɐݒ肵�܂����B�o���邱�ƂȂ�����Ə����ɋ߂Â������̂ł����A�����̘c�݂��傫���Ȃ�߂��đ����������������Ȃ��Ă��܂��܂��B�����̋�����������x�����ł���悤�ɂ��邽�߂ɂ́A���̒��x�͕K�v�ł���Ɣ��f��������ł��B�ǂ�������������Ɠ����̈����������������킹�ɂȂ邱�Ƃ�����Ȃ���Ȃ�܂���̂ŁA���x������Ƃ������Ƃł��B
�@
���̖ڕW�͈����������ɗ͌��炷���Ƃł����A������͂��낤���ċy��_�Ɋ��荞�Ƃ��������ł��B�s�^�S���X�̂R�x��舫���Ȃ��R�x�ƁA���S���������ǂ��T�x�̋����Ƃ������ƂŁA�T�x�́|�Q�܂łƂ��A�R�x�́{�V�܂łɗ��߂܂����B�e���Ă݂Ă���͂��肬��̐����Ɗ����܂������A�F�X�ȗv���Ŏ��ۂ͌x�������z���Ă��܂����Ƃ��N����ł��낤�Ɗ����܂����B
���ϗ��Ɋ���Ă��鎄�B�ɂ́A�ÓT�����͗ǂ�����������Ƃ��������A�����������̂ق����C�ɂȂ�̂ł͂Ȃ����Ƃ����C�����Ă��܂��B���̂Ȃ�A����Ă��镽�ϗ�����ԑ��肪�����ȉ���������ł��B�����̂Ȃ�����������������A���������������R�̎�ނ����ꂽ�����́A�ǂ����������e�͈͂Ɏ��߂邱�Ƃ��ł��Ȃ��������ł͂Ȃ����Ƃ��l�����܂��B
��������������낤�Ƃ�������肭�������A���������������炷�����ŏI�������̂ł͂Ȃ��ł��傤���B
�@
��O�̖ڕW�ł���A�ǂ������i�ǂ��g���a���ɔz�u���邱�Ƃɂ��ẮA�v��ʂ��肭�ł����Ǝv���܂����B�������ł̒��R�a���ŋ�����ǂ����A�����̒��ŋ����Ă��炤��ł����A���ɃV���[�v�U�`�X�i�t���b�g�R�`�U�j�܂ł��������Ȃ�܂��B�ʂ̌�����������A�ቹ���R�{�̊J�����������Ƃ��钷�O�a�����������Ȃ������Ƃł��B
�@
��l�̖ڕW�͒������ł̋��������܂��鎖�ł����A�������r�I��肭�ł����Ǝv���܂��B�ЂƂ̒��ł��F�X�Șa�����g���܂��̂ŁA�M�N�V���N���Ȃ��悤�Ɏg�p�p�x�̍�����v�Șa���̋��������荇�킹�Ă����K�v������܂��B
��܂̖ڕW�̓M�^�[�̃t���b�g���Ȃ�߂��ĉ��t���ɂ����Ȃ�Ȃ��悤�Ɍv�悵�����Ƃł����A����������Ɋ���đS���C�ɂȂ�Ȃ����̂ł����B�������̋Ȃ���ǂ̂��炢�Ɍv�悵����ǂ��̂���������܂���ł������A�ߋ��̌o������Smm�����x�ł͂Ȃ����ƁA�M�^�[����Ƃ̓c�����l������A�h�o�C�X���v���܂����B���̈�ۂł͂����Pmm���炢�Ȃ��Ă����v�ł͂Ȃ����Ǝv���܂����B
���̂悤�ɂ��āA���̖ڕW�����ȍ~�̗v�f�ɂ���āA�v�f���ǂ�ǂ�k������C������Ă����A�e��̌ÓT�����Ɣ�r���Ă݂�ƁA�ڗ������Ȃ��Ȃ������đ�l���������Ƃ��Ċ��������Ƃ�����ۂ��c��܂����B���̎�����ʂ��Ĉ�d�v�Ȏ����킩��܂����B�M�^�[�͐F�X�Ȋy��Ɣ�r���Ă݂Ă��{�����L���ɖ�܂����A���ꂪ�M�^�[�̖��͂̑傫�ȗv�f�ƂȂ��Ă��܂��B���̐�������A���܂菃���ȋ������痣��Ă��܂��ƁA���͂��������Ă��܂��Ƃ������Ƃł��B���ɊJ�����̉��������ƍ�������߂���ƁA�����������ł��^��������Ă��܂����ƂɂȂ�A�ǂ����ʂɂȂ�܂���B�U�{�̌����J�����Ńo�����ƒe�������ɁA�����u���Ȃ�v�ŋ��������肵�Ă��Ȃ���A���t����C�ɂ��Ȃ�Ȃ��ł��傤�B���̓_�o�C�I�����͊��S�T�x�ł�����A�����͈Ղ����������������Ȃ�܂����A�J�����͂��܂�g���܂���B�M�^�[�ł͘a����e���W��A�J�������g�p���Ȃ��Ɖ��t�����ȏ�����傫���Ȃ��Ă��܂��܂��B
�M�^�[�̓��������炽�߂ĔF��������ꂽ���Ƃł����B
�V������̌����čl��������
�����̋^��ł������u���ϗ������ꂾ�����y�����ɂ�������炸�A���̐V���ȉ��������߂���̂��v�Ƃ�������́A���j��{�ł͒N�������Ă͂���܂��A�܂����g�ł������f�ł��Ȃ����Ƃ��ƍl���āA����̎����ɍs�����ڂ��܂����B
���ǂ̂Ƃ��뎄�����_�t�����̂́A�u�I���O�̃n�����j�A�_���瑱�������̗��j�́A�����ȋ��������߂��������ł����A���̌��ʂƂ��đ����������������ł����炷�����Ɍ������A���ϗ��ɒH��t�����̂�����ǁA�����ȋ����ɑ���~���͏����Ă��Ȃ��̂��v�Ƃ������Ƃł����B
�����Z���k�����ϗ�����̐����Ƃ��Ĕ��\���Ă���Q�O�O�N���̊ԁA�M�^�[�Ȃǂ̈ꕔ�̊y��̉����Ƃ��Ďg�p���ꂽ����ǂ��A���y��ʂ̕W�������Ƃ��ėe�ՂɎ�����Ȃ������̂́A�����̋����ɑ���M����������ł���A���̎v����f����Ȃ������������̐l�Ɏc���Ă�������ł͂Ȃ��������Ǝv���Ă��܂��܂��B
�����ĕ��ϗ����s�̃s�A�m�̕W�������Ƃ��Ďg�p���ꂽ���Ƃŕ��y�͂�������ǁA���̌�X�ɂP�T�O�N�ȏ���o���ł��A�ÓT������ɂ��ސl�������ł��ꐶ�������Ă���Ƃ������Ƃł��傤�B����������ƁA�M�^�[���ȈՊy��Ƃ��Ă̕]�������������R�͂����ɂ��������̂ł͂Ȃ����Ǝv���ĂȂ�܂���B
�܂�A�ςȌ����������܂����A���ϗ�����ʂɔF�߂���܂ł̊Ԃ́A�M�^�[�͂��������ȉ����ł�����Ƃ����������o�����A�ȈՂȂ��V�ъy�킾�Ƃ������₩�Ȍ���������Ă����̂ł͂Ȃ����Ǝv���܂��B��\���I�ɓ����Ă��炻�̎��������������ƂŃM�^�[�̖��͂��F������A�Љ�I�ɔF�m�����悤�ɂȂ����̂ł͂Ȃ��ł��傤���B
�����M�^�[���n�߂����́A�ᑭ�Ȋy��ł���Ƃ̃C���[�W���N���V�b�N���y�̐��E�ɂ͎c���Ă����悤�ɋL�����Ă��܂��B�����g�͂��̃M�^�[�p�����������M�^�[�����ʓI�ɔ������������鉹���ł���Ǝv���Ă��܂��B
���̒��x�͂��ꂼ��̊������̓x���ňقȂ�Ƃ͂����A���̋����ɓ����ł���ɏ]���āA���g���@���ɕ��ϗ��̋����Ɋ���Ă��܂��Ă�������ɐɊ�����悤�ɂȂ�܂����B
�g�p�������z������ƁA����͍D�݂̖��ɂȂ�ł��낤�Ƃ����C�����܂����B���R�A���͏����ł��������������Ȃ鎖��]�݂܂����A���̑㏞�͒����ɑ���Ȑ_�o�����Ղ���ł��낤���Ƃł��B����l�́A���ꂾ���̋�J�����Ă��̒��x�̋����ł͊���ɍ���Ȃ��Ǝv�������m��܂���B�ł����璲���Ɏ��M�̂Ȃ��l�ɂ͊��߂邱�Ƃ��ł��܂���B���݂͓d�q�`���[�i�[���g���l�������܂����̂ŁA���̋@�B���ǂ����_�ɂȂ邱�Ƃł��傤���A���ꂾ���ʼn������Ȃ��Ƃ��낪���ł��B���������킷�����͒��������ł͂Ȃ��A���̕s�ǂ≟���Z�p���֘A���܂��̂ŁA������x�̉��t�Z�p���������l�����̉����ɋ��������������ɂ����A�����Ă݂鉿�l������悤�Ɏv���܂��B
�@
��������ς���A�v���X�w���̍l�����ŁA�Ⴆ�����ł�����������������̂Ȃ瑽���̋�J�����Ƃ�Ȃ����A������x�̑���������l�ƁA����Ƃ͋t�ɔ�����������Nj�������́A�\�Ȍ�����������������炷���Ƃ��D�悳���ׂ����ƍl����l�Ƃ̑Η��ɂȂ�ł��낤�Ǝv���܂��B
�������Ƃ́A����Ȃǂ���Ƃ��]����������镪��_�ɂ�����ł���悤�Ɏv���܂��B���ϗ��Ə����ȋ����̑Η��́A�����̗��j�Ɠ��������ő��݂����Ǝ��͍l���Ă��܂��B�����_�����݂Ɣ�ׂĖ����B�̃M���V�������̎���ł��A�A���X�g�N�Z�m�X�̂悤�ȕ��ϗ��ɒʂ���l����������l�����܂������A�����ł̌�������{�̘a�Z�Ƃɂ�錤���Ȃǂ�����܂�����A���l�b�T���X���ȍ~�̉����j�����łȂ��A�e�����ʂ��đ���𒆗f�Ȓ��x�ɗ������悤�Ƃ���ӎv�͑��݂��Ă����Ǝv���܂��B
���݂ɉ����邱�̗��҂̎咣�́A�o���̑��_���Y���Ă���悤�Ɋ����Ă��܂��B�����ȋ�����������Ɗ����Ȃ��l������̂ł��傤���B��������Ƃ���A���̔������͌X�l�̚n�D�̖��ƂȂ��Ă��܂��܂�����A���������c�_�ɂ͂Ȃ蓾�܂���B�ł�����A�����̋����͐l�Ԃ̊����Ƃ��Ắu�������Ɗ�����v�Ƌ��ʗ����������Ƃ���n�܂�ׂ����̂��Ǝv���܂��B���̔������Ƃ͐S�n���ǂ��ƌ��������邱�Ƃ��ł���ł��傤�B
�@
����A�����������Ƃ������s���ȋ������ǂ̒��x�Ȃ�䖝�ł��邩�Ƃ������ɂȂ�܂��ƁA������l�����傫�����̂Ǝv���܂��̂ŁA�e��̉����x���҂̘_�������܂�邱�ƂɂȂ�܂��B�ł�����A���ϗ��̐���_�͊����̖��Ƃ�����́A�����\���̕��@�_��@�\�_�Ƃ��Ę_�c�����ׂ��b��ł���悤�Ɏv���܂��B
���R���̏ꍇ�ł����ʂ̔F���͔����������̖ڕW�ƂȂ炴������܂��A�l�Ԃ̊��o�̖��łȂ��A�y��̎�ނɂ���ēK�ȉ����͈قȂ邱�Ƃ͊m���ł�����A�F�����ɂ��ĕ��ϗ����ǂ��Ƃ����l����������܂����A���ꂼ��̊y��̎���ɍ��킹�āA��������������I�������ق����ǂ��̂ł͂Ȃ����Ƃ����l�������o���܂��B�܂�A������̖ڕW�Ƃ��Ăǂ̂悤�Ȃ����ʼn��y���Č����邩�ɂ���āA�K�ȉ�����I�ׂΗǂ��̂ł͂Ȃ����Ǝ��͍l�����ł��B�s�^�S���X�����͏����T�x�ɁA���S�����͏������R�x�ɓ������������ł��B���Z�R�x���d�˂�Ί��S�T�x�ł����A�����ȋ��������߂���x���͒��R�x���T�x���{�������ł͂Ȃ����ƍl�����܂��B���ϗ��ł͂T�x�Ɂu���Ȃ�v�������܂��A���R�x�ɂ͂S�`�T�������܂��B��������x�ɂł��Ȃ����Ƃ������Ƃ����̎����̉B�ꂽ�e�[�}�ł�����A�ԈႢ�ł͂Ȃ������Ǝ��͊m�M�ł��܂����B
�P�b�ԂɂP�`�Q����x�́u���Ȃ�v�̐��͕s���������ނ���S�n�������Ǝv���̂ł����F�l�͂ǂ���������ł��傤���B�ƂĂ��������Ƃ������B�u���[�g�̂悤�ŁA�a���������f�B�[����������݁A�����D�����h�炷��肩���̂悤�Ȋ����ŁA�����ƌ����Ε����ꂽ�Ԏq����e�ɂ��₳��Ă���悤�ȐS�n�悳������Ǝv���܂��B�ŋ߂̉��y�ł͂T�x�̋����𒆐S�ɂ��ċT�x�̘a��������������邱�Ƃ��A���ϗ��������炵�����ʂ̂悤�ȋC�����Ă��܂��B
�M�^�[�̏����ɂ���
�����ȂƂ���A���̂悤�Ȃ��̂�����Ăǂꂾ���̈Ⴂ������̂��Ƌ^��Ɋ�����l�������ł��傤���A���������������߂�Փ��ɂ͒�R�ł��Ȃ��v�f������܂��B���݂́A�s������������悤�ȕǂ������y����̒��ŁA�Â�������V���������������߂Č����Ɍ������Ă���l������ƕ����܂��B
�ŋ߂ł́A���m�����ōs��ꂽ���q�@�����y����g�p�����R���T�[�g����悳��܂������A�c�O�Ȃ��玄�͂��̂��Ƃ�m��܂���ł������璮�����Ƃ��ł��܂���ł����B�@�����ΐ����Ă݂������y�ł��B
�M�^�[�ł́A�W�����E�V���i�C�_�[���t���b�g�E�{�[�h�������ł���悤�ɉ��ǂ����M�^�[�ŁA��������~�[���E�g�[���ʼn��t�ł���悤�ɂ��A�������Ă���Ƃ������Ƃł��B�V���ȕ��𐁂����邱�ƂɂȂ�̂������������Ă��܂��B
�@
���̔��ʁA�M�^�[�͖����ɉ��ǂ��i�݈قȂ�^�C�v�̊y�킪���B���Ă��āA�M�^�[���Ƃ����\���܂ł���܂��B���B���g���Ă���N���V�b�N�M�^�[�͂ǂ��Ȃ��Ă����̂ł��傤���B�������̉����̂��Ƃ�����Ă��鎞�Ɋ��������Ƃ́A��O���X�̂悤�Ȃ��̂Ȃ̂����m��܂��A�M�^�[�͑f�G�Ȋy�킾�Ƃ������Ƃł����B����l�͕��ϗ����L�܂������ƂŁA���Ē����������Ă����F�ʊ��͂Ȃ��Ȃ�A��ꉻ���ꂽ���������œ]�������Ă������������ω����邾���̖��C�Ȃ����̂ɂȂ��Ă��܂����ƌ����܂��B������������ꂽ�F�ʊ��̓I�[�P�X�g�����y�̔��W�ɂƂ��Ȃ��A���l�Ȋy��̑g�����ɂ�薄�ߍ��킳��Ă����Ƃ����܂��B
���ϗ��s�A�m�����y�������Ƃɂ�镾�Q�Ƃ��Ă̖ʂ��Ƃ炦�Ă��������l�������������ŁA�����t�̃A�j�^�T��T�����@���͂��������ӌ��ɔ��Ȃ悤�ŁA���ϗ��͗��j���I�����Ȃ̂��Ɣ��_���Ă��܂��B���y�ɑ���l�Ԃ̗~���̒��ɁA�s�����Ő��������Ȃ��v�f���ɋ��߂Ă�����͎����s�\�ł���A�����̔������Ɠ]���̗e�Ղ��Ɖ��t�̉\�ȗv�f�͓����ɐ��������Ȃ����炱���A���ϗ����c�����̂��ƌ��������ł��B
���̍l���͂���Ƃ͏�������Ă��āA�܂����ꂩ��������͂ǂ̂悤�ɕω����邩������Ȃ��ŁA�����������疂�@�̂悤�Ȃ����ŏ����ȋ����Ŏ��݂ȓ]�����\�ȗ��_���o�����邩������Ȃ��Ƃ��v���܂��B
�@
���Ƃ��ƃ����Z���k����̐��l�Ƃ��Ĕ��\�������ƂŁA�t���b�g�����y��ł͕��ϗ����ŗǂ̉����ł���Ƃ��ăM�^�[�͍���Ă����킯�ł����A�O���I�����肩��M�^�[�Ƃ����y�킪���y�V�[����Ȋ����Ă������Ƃ͎����ł��B
�d�C�M�^�[�̑傫�ȉe���͂�����܂����A���_�ϗ��ɖ߂��Ă݂�A���ϗ������y����̂ƌĉ����ăM�^�[�����s�����Ƃ������Ƃ������ł��B
���Ƃ͂Ƃ����s�A�m�����y���n�߂��P�X���I�㔼�ɁA�s�A�m�̊�{�����Ƃ��č̗p����Ă��畽�ϗ��͈�ʓI�ȉ����Ƃ��Ă̒n�ʂ��m�����܂����B
���̗���ɏ�����`�ŋ��R���ۂ��͕ʂƂ��āA�M�^�[�����ڂ����悤�ɂȂ������Ƃ������ł��B
���̂��ƍl�������A�P���Ɏ��������̃M�^�[��I���Ƃ����_�ɗ����Ԃ��čl����ƁA����̓M�^�[�̉��F���������Ɗ����A�D���ɂȂ�������ł��B
�@�l���Ă��݂�Ύ��ɕs�v�c�Ȋy��ł��B���ɂ���ĉ��F���قȂ邵�A����̃|�W�V�����ɂ���Ă��ς�B�E��̒e���ʒu��p�x�ł��قȂ�A�t�@�����푽�l�ł��B�s�A�m�ɂ͂Ȃ��|���^�����g��X���[�⃔�B�u���[�g���ł��܂��B�V���v��������ǂ��Ƒt�y��Ƃ��Ă��\���ʗp���邵�A�Ŋy��I�Ȍ��ʂ��o���鉽�ł����̂悤�ȂƂ炦���̂Ȃ��y�킾�Ƃ������܂��B���ʂ͏���������ǂ��_�C�i�~�b�N�����W�͍L���Ǝv�����A����Ȗ��؋��̂悤�ȐF�ʊ��Ɉ�ꂽ�y��͓d�C�y��������I�[�P�X�g���ȊO�ɂ͂Ȃ��ł��傤�B
���̕ό����݂ȉ��F�≹���̕ω������y�ł̑��ʂȐS�ە\�����\�ɂ�����̂ŁA���h���[�S�������u�M�^�[�̍��v���̂��̂��Ǝv���Ă��܂��B
����Ȋy�킾���炱�����E���̐l�X�̐S���Ƃ炦���̂��낤�Ǝv���ĂȂ�܂���B���̃M�^�[�Ɏg���Ă��鉹�������ϗ��ł���Ȃ���A�M�^�[���y��������Ȃ��Ɗ�����l���ǂꂾ������̂ł��傤���B
�@
�s�A�m�x���҂ɂ͐\����Ȃ�����ǂ��A����̕��ϗ��ɑ���ᔻ�̌��t��ے肵�Ȃ���A�M�^�[�����y���������̓s�A�m�̕��y�ɔ������ϗ��������炵�����������鉹�y��n�ɁA�M�^�[�̑@�ׂő��ʂȕ\���͂����ɍ炫�ւ�����ʂ̉Ԕ��̂悤�ɉ��y���E���ʂ�A�����̐l�X�Ɏ����ꂽ���Ƃł͂Ȃ����Ǝv���Ă��܂��̂ł��B�܂�A�I�[�P�X�g�����ʂ��������������͉A�ŃM�^�[���x���Ă����̂��ƌ����Ȃ����Ȃ��̂ł͂Ȃ��ł��傤���B
�@
���͕��ϗ��̋����ɖ������Ă͂��܂��A����ł��悭�ł����������Ǝv���܂��B���R�M�^�[�ł����ϗ��ɓ��L�ȂR�x�͕������܂����A����ł��������Ȃ��Ɗ����邱�Ƃ͂���܂���B�T�x�̋����͑�ςɔ��������̂ł����A����������ƃM�^�[�ł͉��t���ɑt�҂������ȉ����𑀍삵�āA�����ł������ɋ߂Â��悤�Ɩ��ӎ��ɕω������Ă���̂ł��낤�ƍl���Ă��܂��B
�܂����ꂪ�\�ł���Ƃ��낪�M�^�[�̐��ݔ\�͂̒�m��Ȃ������ł�����Ǝv���܂��B
�Ƃ�����A�M�^�[�͂���ȗ��j�Ɗ��̒��Ő��܂���������̒����ł���悤�ȋC�����Ă��܂��B
�P�Q���̉��y���s���l�܂����������������ŁA�����ȋ����ɉ�A�������ȉ_�s�����f���܂����A�M�^�[�̏�������z�����ϗ��̓M�^�[�̂�肩���ł���Ɗ����Ă��܂��B
�@- ����� -�@�@�@
���P�F���ϗ��̐����ɂ��Ă͏�������悤�ŁA�����������Ă��ʔ����ł��傤�B�I���O�̃A���X�g�N�Z�m�X�����肩��n�܂��āA�Â����̂͒����ł̌����A�����ă��[���b�p�ɂ�����ÓT�����j�ɓo�ꂷ�鑽���̗��_�Ƃ������A���ϗ����ߑ�ɂ����ēˑR�ƒa�������̂ł͂Ȃ����Ƃ��킩��܂��B
�s�NjL�t
�P�D���܂łɍ��ꂽ�~�[���g�[���E�M�^�[�͍����ɑΉ�����t���b�g�����������lj�����Ă��Ȃ��̂ŁA���̃_�u���t���b�g�ł͑��߂���̂ł͂Ȃ����Ǝv���邩������܂���B
�����ł͗~�����Ĕ������剹�Ƃ��钲�ɂ����āA�P�Q���̑S�Ă����Ȃ��o����悤�ɍl�������ʂŁA���̊y��͂P�I�N�^�[���ɂP�X���̍\���ł��B�ʏ�̂P�Q�t���b�g�ŃY������������ꏊ�͂S�����ł�����A���̃t���b�g�����lj����ĂP�U�t���b�g�̍\���ɂ��邱�Ƃ��A�g�p�ł��钲���������Ȃ�܂��������I�ȑI�����ł��傤�B�����͂S�������t���b�g����Đݒu����A�P�Q���̐��K�ȃ~�[���g�[�������ɂȂ�܂��B
�n�C�|�W�V�����ł̓t���b�g�Ԋu�������Ȃ邽�߁A�Ԉ������Ƃ��l���Ă�������������܂��A�����I�Ƀt���b�g�̈ꕔ������Ă�������������܂���B���̏ꍇ�A���S�ɊԈ������t���b�g���I�ɕ��������Ă������ł��傤�B���̃_�u���E�t���b�g�͍\�z�i�K�̂��̂ł�����A���̊y��삳��Ă��y��Ƃ��Ă̕s��������邱�Ƃ͓��R�ɍl�����܂����A�����ł͐ӔC���܂���̂ŁA���ȐӔC�͈̔͂Ő��삵�Ă��������B
�_�u���t���b�g�̃t���b�g�ʒu�v�Z�́A�[�������̊W�Ŗ����̐��l�����m�Ȍv�Z���l�Ǝ�قȂ�ꍇ������܂��B
�Q�D�t���b�g�̋Ȃ��ɂ��ẮA�l�����≉�t���e�ɂ���ċ��e�͈͂��قȂ��Ă���Ǝv���܂��B���������ȌÓT�������g�p�������Ȃ�A�M�^�[�ł̓��@���b�e�B�������O�A�����̓P���i�[�����肪�g���₷���ł��傤�B
�����O�͂e�`�`�܂ł͖��Ȃ��������ł����A�a�A�d�����ϗ����x�ł������Ԍ����Ă���Ǝv���܂��B�P�t���b�g�����͋Ȃ肪�傫���̂ł����A���Ƃ͖��Ȃ��ł��傤�B���@���b�e�B�͂e�����S���ƂȂ��Ă��āA�����O�̂b���S�����P�t���b�g�n�ɂȂ�܂����A�Ȃ肪�����������Ȃ�܂��B�S�t���b�g����ԍL���A
�U�T�Omm�̌����łS�D�Wmm�ł����A�\���Ɏg�p�ł���̂ł͂Ȃ����Ǝv���܂��B
�R�D���̃e�L�X�g�ł̓o�b�n�̉������Љ�Ă��܂����A����͎������ϗ��N�����B�[�A�ȏW�̎��M���\���ɕ`���ꂽ�����͗l��ǂ݉����A���̓��e����\�����������ł���A���Ԉ�ʂɂ͐����ɔF�m����Ă�����̂ł͂���܂���B
���̓��e�ٕ͐��u�o�b�n�̉����͂��ꂾ�I�v�œ���������Ă��܂��̂ŁA�����̂�����͂������������B
�S�D���̃e�L�X�g�͂Q�O�O�S�N�H�Ƀ_�u���t���b�g���\�z������ŁA�����̘b�����邽�ɂ߂܂Ƃ߂����̂����S�ƂȂ��Ă��邽�߁A�r���������������Ƃ������͂܂�����܂���ł������A���������M�^�[�Ɋւ��镔���́A�Q�O�O�W�N�Ɏ��ۂɊy�퐻��Ɏ�肩����O��ɉ��M�C�����܂����̂ŁA���͕\���ł̎��n�������Ȃ�����������܂��B���������M�^�[�͂r���������������u���Ӂv���g�p������P���̊y��ł���A���̊y��ɂ���ۂ𐳒��ɏ����܂����B
���݂͑�Q���́u����v�����������Ƃ���ł����A������\�z�ǂ���̌��ʂƂȂ�܂����B
��؉����͂P�ł͂Ȃ��A���̉����ȊO�ɂ��M�^�[�̂��߂̉����Ƃ��ē����v�ڕW������������������܂��̂ŁA�u��؉����ɂ����v�Ƃ����ٕ��ʼn�����Ă��܂��̂ŁA�����̂�����͂�������������������B
�T�D���̉������g�p���Đ��삳�����́A���L�Ɍ�����悤���肢�\���グ�܂��B
e-mail�Fsuzukimasaru@m6.dion.ne.jp
�����Q�Q�N�R���Q�P���@�t���̓��� �@�@�@���ӁF��@��
Back�@�@�@�@�@�@�@�@�@Home
|